Теорема. Пусть функции u=u(x) и v=v(x) дифференцируемы на некотором интервале (а;в). Пусть на (а;в) функции v(x)*u’(х) имеет первообразную, тогда на интервале (а;в) функция v’(x)*u(x) так же имеет первообразную, при этом справедливо равенство ∫u(x)*v’(x)dx=u(x)*v(x) - ∫u’(x)*v(x)dx (1).
Замечание. Определение дифференциала и свойство инвариантности его формы позволяют придать формуле (1) следующий вид ∫u*dv=u*v - ∫v*du (2).
Интегралы, вычисляемые таким методом:
1)интегралы, к которых подынтегральная функция содержит одну из следующих функций: arcsinX, lnX, arccosX, arctgX, arcctgX, ln2X, lnu(x), arcsin2X, arccos2X, arctg2X, arcctg2X. При условии. Что оставшаяся часть подынтегральной функции представляет собой производную известной функции.
2)интегралы вида:
1.∫(ax+b)n*cosXdx; 2. ∫(ax+b)n*sinXdx; 3.∫(ax+b)n*eaxdx; 4.∫(ax+b)n*aαxdx, при а,в=const.
Эти интегралы беруться путем последовательного n-кратного применения формулы (1) или (2), где всякий раз в качестве u(x) надо выбирать а+в в соответствующей степени. После каждого интегрирования эта степень будет уменьшаться на единицу.
3)∫eαx*cosβxdx; ∫eαx*sinβxdx; ∫aαx*cosβxdx; ∫aαx*sinβxdx; ∫sin(lnX)dx; ∫cos(lnX)dx, при α,β,а=const.
Такие интегралы берутся в двухкратном интегрировании по частям, при любом выборе u(x).
15. Пусть требуется вычислить 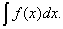
Предположим, что существуют дифференцируемые функции 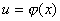 и
и 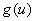 , такие, что
, такие, что 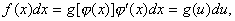 тогда
тогда 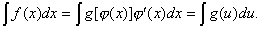
Указанное преобразование подынтегрального выражения называют подведением под знак дифференциала.
Например. 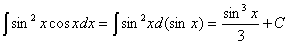 .
.
Замечание. При интегрировании методом подведения под знак дифференциала бывают полезны следующие равенства:
1. 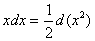 ;
;
2. 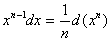 ;
;
3. 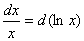 ;
;
4. 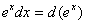 ;
;
5. 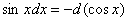 ;
;
6. 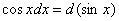 ;
;
7. 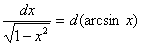 ;
;
8. 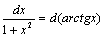 ;
;
9. 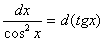 ;
;
10. 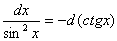 ;
;
11. 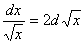 .
.
 2015-05-30
2015-05-30 751
751








