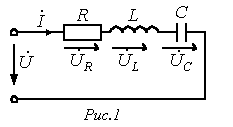 Для цепи на рис.1 имеет место
Для цепи на рис.1 имеет место
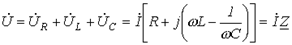
где
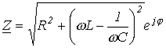 ; ; | (1) |
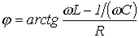 . . | (2) |
В зависимости от соотношения величин 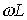 и
и 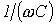 возможны три различных случая.
возможны три различных случая.
1. В цепи преобладает индуктивность, т.е. 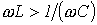 , а следовательно,
, а следовательно,
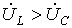 . Этому режиму соответствует векторная диаграмма на рис. 2,а.
. Этому режиму соответствует векторная диаграмма на рис. 2,а.
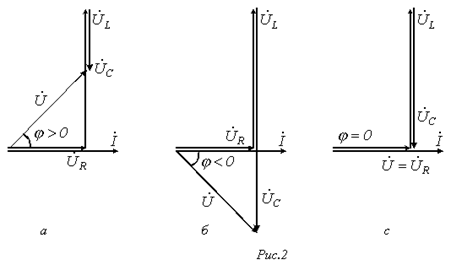
2. В цепи преобладает емкость, т.е. 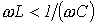 , а значит,
, а значит, 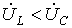 . Этот случай отражает векторная диаграмма на рис. 2,б.
. Этот случай отражает векторная диаграмма на рис. 2,б.
3. 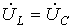 - случай резонанса напряжений (рис. 2,в).
- случай резонанса напряжений (рис. 2,в).
Условие резонанса напряжений
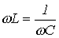 . . | (3) |
При этом, как следует из (1) и (2), 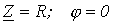 .
.
При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания.
Пусть, например, в цепи на рис. 1 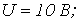
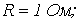
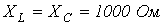 . Тогда
. Тогда 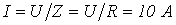 , и, соответственно,
, и, соответственно, 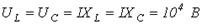 .
.
Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков.
Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной.
Суть дела не меняется, если в цепи имеется несколько индуктивных и емкостных элементов. Действительно, в этом случае 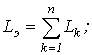
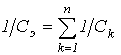 , и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ .
, и соотношение (3) выполняется для эквивалентных значений LЭ и CЭ .
Как показывает анализ уравнения (3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (3) для резонансной частоты можно записать
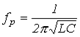 . . | (4) |
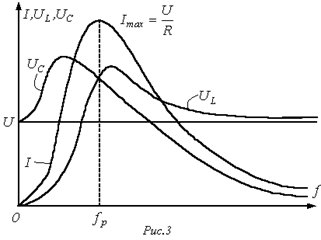
Резонансными кривыми называются зависимости тока и напряжения от частоты. В качестве их примера на рис. 3 приведены типовые кривые I(f); 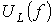 и
и 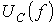 для цепи на рис. 1 при U=const.
для цепи на рис. 1 при U=const.
Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:
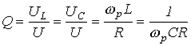 , , | (5) |
- и характеризующая “избирательные” свойства резонансного контура, в частности его полосу пропускания 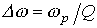 .
.
Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением
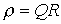 , , | (6) |
или с учетом (4) и (5) для 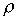 можно записать:
можно записать:
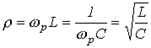 . . | (7) |
 2015-05-30
2015-05-30 1208
1208
