Резонансные кривые тока и напряжения

Рисунок 11.5

Рисунок 11.4

Рисунок 11.3

Рисунок 11.2

Рисунок 11.1

Кривая, которая соединяет концы векторов 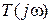, носит название годографа передаточной функции (годографом амплитудно-фазовой характеристики). Годограф строят при изменении частоты от нуля к бесконечности.

Пример. Определить комплексный коэффициент передачи по напряжению 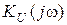, АЧХ и ФЧХ для схемы (рис.11.2а).

Согласно с определением: 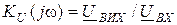. Задача решается в такой последовательности: 1) задаемся 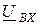; 2) определяем комплексное значение выходного напряжения по закону Ома:

;

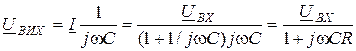3) находим ;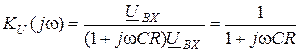

4) подаем 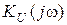в показательной форме, находим АЧХ и ФЧХ (рис.11.2б,в):

.

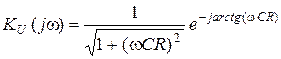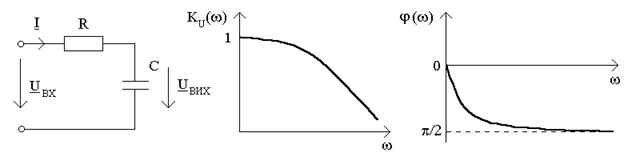
а) б) в)

11.2 Последовательный резонансный контур. Определение и условия резонанса

Колебательный контур - электрический круг, в котором возможны колебание свободной составной тока. Резонансный контур - электрическая цепь, в которой имеет место явление резонанса (напряжений или токов).

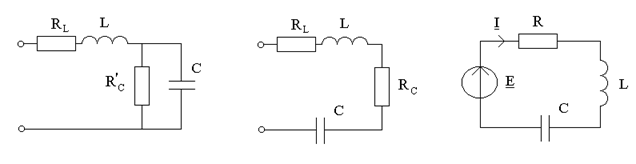
Последовательный резонансный контур - резонансный контур, который состоит из индуктивного и емкостного элементов, соединенных последовательно (рис.11.3а,б). На схеме (рис.11.3в) R, L, C - первичные параметры контура, причем 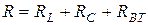, где 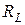- активное сопротивление катушки индуктивности, 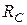- сопротивление растекания конденсатора, перерасчитанное в последовательное соединение, 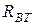- сопротивление проводов (потерь). Чтобы дать определение резонанса, найдем ток в цепи (рис.11.3в):

,

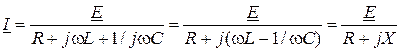где 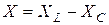- реактивное сопротивление контура.

Запишем комплексное действующее значение тока в показательной форме

,

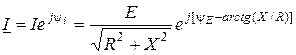где 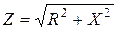- полное сопротивление контура.

Итак, резонанс - это явление в электрической цепи, которая имеет участки с индуктивными и емкостными элементами, по которому разница фаз напряжения и тока на входе цепи равняется нулю.

Из этого определения вытекает, что полное сопротивление контура должно быть активным. Тогда реактивное сопротивление или проводимость цепи, в которой наблюдается резонанс, равняются нулю.

а) б) в)

Итак, если в общем случае действительны соотношения

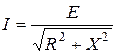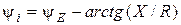; , то при резонансе:

1) 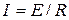- это условие амплитудного резонанса;

2) 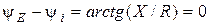; ; 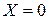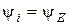- условие возникновения фазового резонанса.

11.3 Вторичные параметры последовательного резонансного контура

1. Резонансная частота - частота тока (напряжения) во время резонанса в цепи. Обозначается 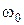и определяется, исходя из условия резонанса X = 0; :

; .

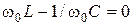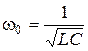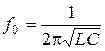Значению циклической частоты 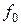соответствует резонансная длина волны:

,

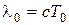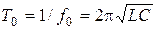
где c - скорость распространение электромагнитных волн.

2. Характеристическое (волновое) сопротивление контура - сопротивление каждого из реактивных элементов при резонансе: .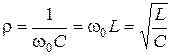

3. Добротность - отношение характеристического сопротивления к активному сопротивлению контура: 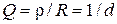, где d - затухание - величина, обратная к добротности, которая характеризует интенсивность затухания колебаний в контуре.

Добротность характеризует длительность собственных колебаний в контуре, ее можно определить также как коэффициент качества, который равняется отношению абсолютного значения реактивной мощности к активной мощности.

4. Полное сопротивление - модуль входного комплексного сопротивления контура Z.

,

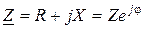где 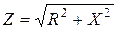- модуль Z;

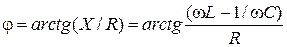- аргумент Z.

Частотные зависимости полного и реактивного сопротивления 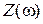, 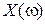изображены на рис.11.4. Из графика видно, что на резонансной частоте реактивное сопротивление контура равняется нулю, а 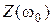равняется сопротивлению потерь R.

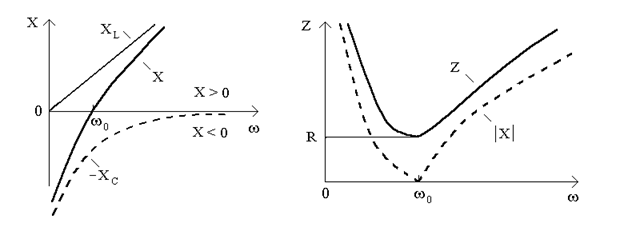
а) б)

5. Фазовая характеристика - зависимость аргумента входного сопротивления последовательного контура от частоты (рис.11.5а): .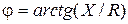

6. Резонансная кривая тока - зависимость модуля комплексного действующего (амплитудного) значения тока от частоты (рис.11.5б):

.

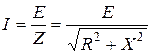Очевидно, что на частоте резонанса 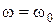, выполняются такие соотношение: , .

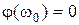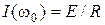11.4 Векторная диаграмма напряжений при резонансе

Запишем для последовательного резонансного контура уравнения по второму закону Кирхгофа:

.

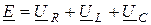Если частота равняется резонансной частоте 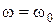, то

,

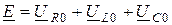где 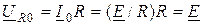- напряжение на сопротивлении R при резонансе;

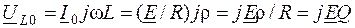- напряжение на индуктивности при резонансе;

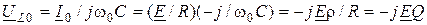- напряжение на емкости при резонансе.

В соответствии с полученными выражениями на рис.11.5в изображена векторная диаграмма тока и напряжений при резонансе. Как видно из рисунка, при 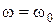выполняются такие соотношения:

1) напряжение на сопротивлении R совпадает по фазе с током I, а модуль 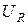равняется значению E; напряжения на реактивных элементах равны между собой по модулю и противоположны по направлению;

2) по абсолютной величине напряжения на реактивных элементах последовательного резонансного контура в Q раз превышают значение ЭДС, которая действует на входе: 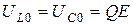. Итак, в последовательном контуре наблюдается резонанс напряжений.

Резонанс напряжений - явление резонанса на участке электрической цепи, в которую входят последовательно соединенные индуктивный и емкостной элементы.

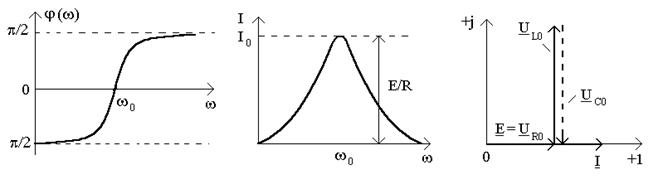
а) б) в)