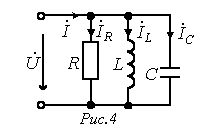
 Для цепи рис. 4 имеем
Для цепи рис. 4 имеем
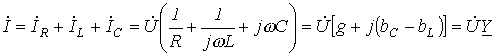 ,
,
где
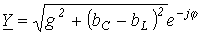 ; ;
| (8) |
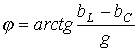 . .
| (9) |
В зависимости от соотношения величин 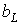 и
и 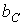 , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
, как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.
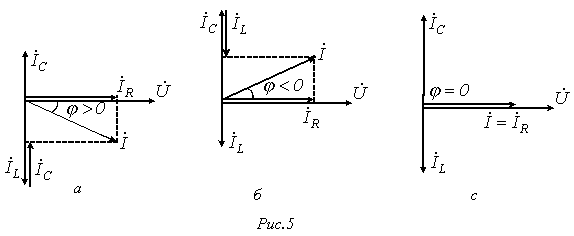
В цепи преобладает индуктивность, т.е. 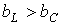 , а следовательно,
, а следовательно, 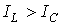 . Этому режиму соответствует векторная диаграмма на рис. 5,а.
. Этому режиму соответствует векторная диаграмма на рис. 5,а.
В цепи преобладает емкость, т.е. 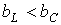 , а значит,
, а значит, 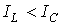 . Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
. Этот случай иллюстрирует векторная диаграмма на рис. 5,б.
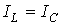 - случай резонанса токов (рис. 5,в).
- случай резонанса токов (рис. 5,в).
Условие резонанса токов 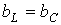 или
или
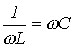 . .
| (10) |
При этом, как следует из (8) и (9), 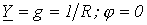 . Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.
. Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности при отсутствии в цепи на рис. 4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.
Идентичность соотношений (3) и (5) указывает, что в обоих случаях резонансная частота определяется соотношением (4). Однако не следует использовать выражение (4) для любой резонансной цепи. Оно справедливо только для простейших схем с последовательным или параллельным соединением индуктивного и емкостного элементов.
При определении резонансной частоты в цепи произвольной конфигурации или, в общем случае, соотношения параметров схемы в режиме резонанса следует исходить из условия вещественности входного сопротивления (входной проводимости) цепи.
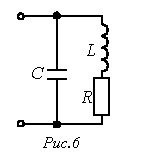 Например, для цепи на рис. 6 имеем
Например, для цепи на рис. 6 имеем
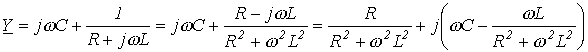
Поскольку в режиме резонанса мнимая часть 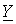 должна быть равна нулю, то условие резонанса имеет вид
должна быть равна нулю, то условие резонанса имеет вид
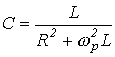 ,
,
откуда, в частности, находится резонансная частота.
 2015-05-30
2015-05-30 1011
1011








