Решение нелинейного уравнения (системы нелинейных уравнений), описывающего (описывающих) состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится следующим образом: на основе первой, достаточно грубой, оценки определяется начальное значение корня (корней), после чего производится уточнение по выбранному алгоритму до вхождения в область заданной погрешности.
Наиболее широкое применение в электротехнике для численного расчета нелинейных резистивных цепей получили метод простой итерации и метод Ньютона-Рафсона, основные сведения о которых приведены в табл. 1.
Таблица 1. Итерационные методы расчета
| Последователь-ность расчета | Геометрическая иллюстрация алгоритма | Условие сходимости итерации | Примечание |
Метод простой итерации
1.Исходное нелинейное уравнение электрической цепи 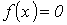 , где , где 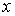 -искомая переменная, представляется в виде -искомая переменная, представляется в виде 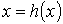 .
2. Производится расчет по алгоритму .
2. Производится расчет по алгоритму 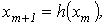 где где 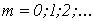 - шаг итерации.
- шаг итерации.
| 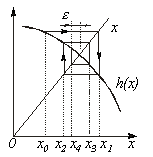 Здесь Здесь 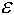 - заданная погрешность - заданная погрешность
| На интервале между приближенным и точным значениями корня должно выполняться неравенство 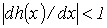
| 1.Начальное приближение 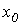 обычно находится из уравнения обычно находится из уравнения 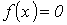 при пренебрежении в нем нелинейными членами.
2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка при пренебрежении в нем нелинейными членами.
2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка
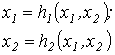 итерационные формулы имеют вид
итерационные формулы имеют вид 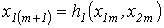 ; ;
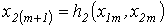 .
3. При решении системы уравнений сходимость обычно проверяется в процессе итерации. .
3. При решении системы уравнений сходимость обычно проверяется в процессе итерации.
|
Метод Ньютона-
-Рафсона
1. На основании исходного нелинейного уравнения электрической цепи 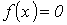 , где , где 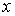 -искомая переменная, записывается итерационная формула -искомая переменная, записывается итерационная формула 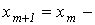 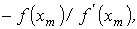 где где 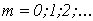 - шаг итерации.
2.По полученной формуле проводится итерационный расчет - шаг итерации.
2.По полученной формуле проводится итерационный расчет
| 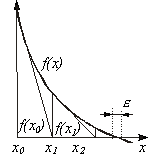 Здесь Здесь 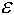 - заданная погрешность - заданная погрешность
| На интервале между приближенным и точным значениями корня должны выполняться неравенства 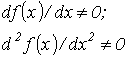
| Примечания п. 1,2 и 3 к методу простой итерации распространимы на метод Ньютона-Рафсона. При этом при решении системы 2-го порядка 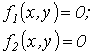 итерационные формулы имеют вид
итерационные формулы имеют вид
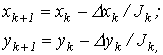 где
где
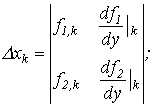 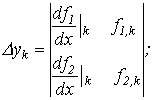
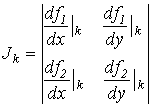
|
 2015-05-30
2015-05-30 638
638







