Существует несколько способов задания функции.
а) Аналитический способ, если функция задана формулой вида 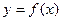 . Этот способ наиболее часто встречается на практике. Так, функция
. Этот способ наиболее часто встречается на практике. Так, функция 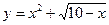 задана аналитически.
задана аналитически.
Не следует смешивать функцию с ее аналитическим выражением. Например, одна функция
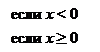
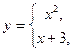
имеет два аналитических выражения: 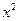 (при
(при 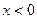 ) и
) и 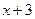 (при
(при 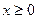 ).
).
б) Табличный способ, если функция задана таблицей, содержащей значения аргумента х и соответствующие значения функции 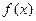 , например таблица логарифмов.
, например таблица логарифмов.
в) Графический способ, если функция изображена в виде графика – множества точек (х,у) плоскости, абсциссы которых есть значения аргумента х, а ординаты которых – соответствующие им значения функции у 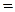 f (x).
f (x).
г) Словесный способ, если функция описана правилом ее составления, например, функция Дирихле: 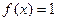 , если х – рационально,
, если х – рационально, 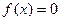 , если – х иррационально.
, если – х иррационально.
д) Функция может быть задана программой, вычисляющей ее значения с помощью компьютера.
Основные свойства функций. К ним относятся четность и нечетность, монотонность, ограниченность, периодичность.
1. Четность и нечетность. Функция 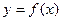 называется четной, если для любых значений х из области определения
называется четной, если для любых значений х из области определения 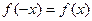 , и нечетной, если
, и нечетной, если 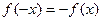 . В противном случае функция
. В противном случае функция 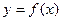 называется функцией общего вида.
называется функцией общего вида.
Например, функция 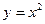 является четной, так как
является четной, так как 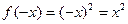 и
и 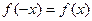 , а функция
, а функция 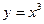 - нечетной, так как
- нечетной, так как 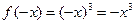 и
и 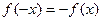 . В то же время, например, функция
. В то же время, например, функция 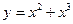 является функцией общего вида, так как
является функцией общего вида, так как 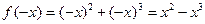 и
и 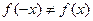 ,
, 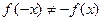 .
.
График четной функции симметричен относительно оси ординат (см., например, график функции 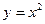 на рис. 4.12), а график нечетной функции симметричен относительно начала координат (см., например, график функции
на рис. 4.12), а график нечетной функции симметричен относительно начала координат (см., например, график функции 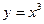 на рис. 4.13).
на рис. 4.13).
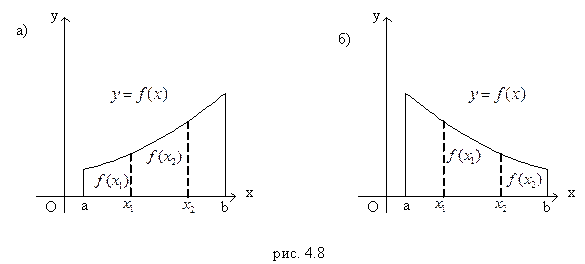 2. Монотонность. Функция
2. Монотонность. Функция 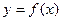 называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 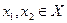 и
и 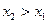 . Тогда функция возрастает на промежутке Х, если
. Тогда функция возрастает на промежутке Х, если 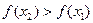 , и убывает, если
, и убывает, если 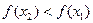 (рис. 4.8).
(рис. 4.8).
Функции, возрастающие и убывающие, называются монотонными функциями. Так, например функция 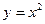 (см. рис. 4.12) при
(см. рис. 4.12) при 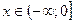 убывает и при
убывает и при 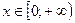 возрастает.
возрастает.
3. Ограниченность. Функция 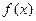 называется ограниченной на промежутке Х, если существует такое положительное число M>0, что
называется ограниченной на промежутке Х, если существует такое положительное число M>0, что 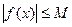 для любого
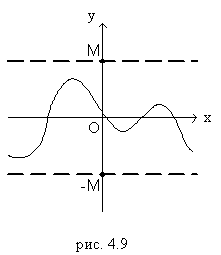
для любого 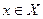 . В противном случае функция называется неограниченной. Например, функция
. В противном случае функция называется неограниченной. Например, функция 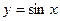 ограничена на всей числовой оси, ибо
ограничена на всей числовой оси, ибо 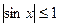 для любого x
для любого x 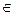 R. (рис. 4.9).
R. (рис. 4.9).
4. Периодичность. Функция 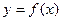 называется периодической с периодом
называется периодической с периодом 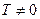 , если для любых х из области определения функций
, если для любых х из области определения функций 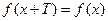 . Например, функция
. Например, функция 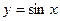 имеет период
имеет период  , так как для любых значений х
, так как для любых значений х 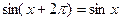 .
.
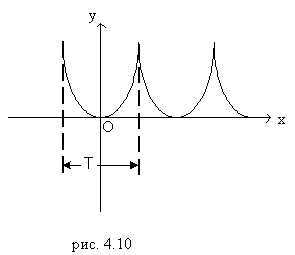
График периодической функции 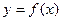 может быть получен сдвигом кривой
может быть получен сдвигом кривой 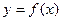 (
(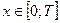 ) вправо (влево) на отрезки Т, 2Т, … (рис. 4.10).
) вправо (влево) на отрезки Т, 2Т, … (рис. 4.10).
Обратная функция. Пусть 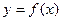 есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому
есть функция от независимой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому 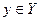 единственное значение
единственное значение 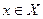 , при котором
, при котором 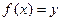 . Тогда полученная функция
. Тогда полученная функция 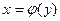 , определенная на множестве Y с областью значений Х, называется обратной.
, определенная на множестве Y с областью значений Х, называется обратной.
Так как традиционно независимую переменную обозначают через х, а функцию – через у, то функция, обратная к функции 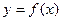 , примет вид
, примет вид 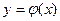 . Обратную функцию
. Обратную функцию 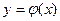 обозначают также в виде
обозначают также в виде 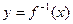 (аналогично с обозначением обратной величины). Например, для функции y
(аналогично с обозначением обратной величины). Например, для функции y 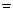 ax обратной будет функция x
ax обратной будет функция x 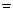 log ay, или (в обычных обозначениях зависимой и независимой переменных)
log ay, или (в обычных обозначениях зависимой и независимой переменных) 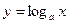 .
.
Можно доказать, что для любой строго монотонной функции 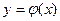 существует обратная функция.
существует обратная функция.
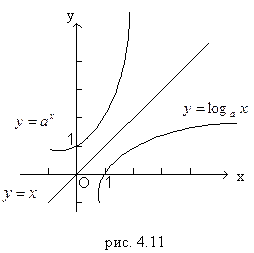 Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (на рис. 4.11 показаны графики взаимно обратных функций 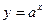 и
и 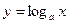 при
при 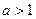 ).
).
Сложная функция. Пусть функция 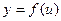 есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией
есть функция от переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь? является функцией 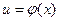 от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция
от переменной х, определенной на множестве Х с областью значений U. Тогда заданная на множестве Х функция 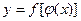 называется сложной функцией (функцией от функции). Например,
называется сложной функцией (функцией от функции). Например, 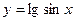 - сложная функция, так как ее можно представить в виде
- сложная функция, так как ее можно представить в виде  , где
, где 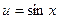 .
.
4.3. Элементарные функции. Классификация функций. Преобразования графиков.
Функция называется явной, если она задана формулой 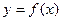 , в которой правая часть не содержит зависимой переменной. Например,
, в которой правая часть не содержит зависимой переменной. Например, 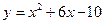 .
.
Функция у называется неявной, если она задана уравнением 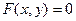 , неразрешенным относительно зависимой переменной. Например,
, неразрешенным относительно зависимой переменной. Например, 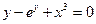 . Иногда функцию, заданную неявно, можно привести к явному виду, иногда это сделать невозможно. Например,
. Иногда функцию, заданную неявно, можно привести к явному виду, иногда это сделать невозможно. Например, 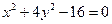 - функция задана неявно. Приведем к явному виду:
- функция задана неявно. Приведем к явному виду: 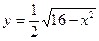 .
.
Графиком уравнения 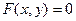 называется множество точек плоскости хОу, координаты которых удовлетворяют этому уравнению.
называется множество точек плоскости хОу, координаты которых удовлетворяют этому уравнению.
 2015-05-30
2015-05-30 5383
5383
