2015-06-10
2378
128. Дискретная случайная величина Х задана законом распределения вероятностей
| Х | |||
| Р | 0,3 | 0,1 | 0,6 |
Значение F (2) равно …
129. Дискретная случайная величина Х задана законом распределения вероятностей
| Х | |||
| Р | 0,1 | 0,5 | 0,4 |
На промежутке (2; 4] функция распределения случайной величины равна…
| 1) | 0 | 3) | 0,4 | 5) | 0,6 | 7) | 1 |
| 2) | 0,1 | 4) | 0,5 | 6) | 0,9 |
130. Стрелок стреляет по мишени 5 раз. Случайная величина Х – количество попаданий в мишень. Значение F (6) равно …
131. Укажите справедливые утверждения для функции распределения случайной величины
| 1) | 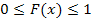 | 3) | 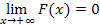 | 5) | 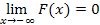 | 7) |  |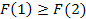
| 2) | 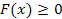 | 4) | 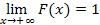 | 6) | 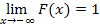 | 8) |  |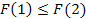
132. Функция распределения дискретной случайной величины имеет вид
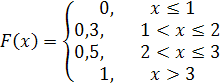
Значение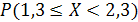 
равно …
133. Случайная величина Х – рост человека, случайно отобранного из группы людей, см. Значение вероятности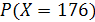 
равно …
134. Х – непрерывная случайная величина, принимающая значения из промежутка [0; 100]. Значение вероятности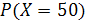 
равно …
135. Функция распределения непрерывной случайной величины имеет вид
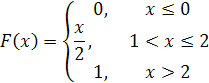
Плотность вероятности этой случайной величины на промежутке 1 < х ≤ 2 равна …
136. Укажите справедливые утверждения для непрерывной случайной величины (F (x) – интегральная функция распределения, j(x) – дифференциальная функция распределения)
| 1) | 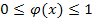 | 3) | 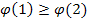 | 5) |  |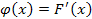
| 2) | 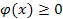 | 4) | 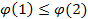 | 6) |  |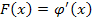
137. Укажите справедливые утверждения для непрерывной случайной величины (F (x) – интегральная функция распределения, j(x) – дифференциальная функция распределения)
| 1) | 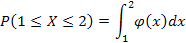 | 3) | 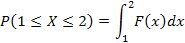 | 5) |  |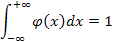
| 2) | 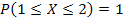 | 4) | 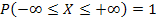 | 6) | |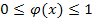
138. Укажите справедливые утверждения для непрерывной случайной величины (F (x) – интегральная функция распределения, j(x) – дифференциальная функция распределения)
| 1) | 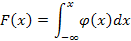 | 4) |  |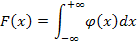
| 2) | 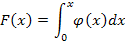 | 5) |  |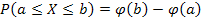
| 3) | 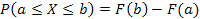 | 6) |  |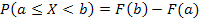
139. Укажите функцию, которая может быть плотностью вероятности некоторой непрерывной случайной величины
| 1) | 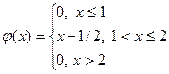 | 3) |  |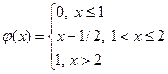
| 2) | 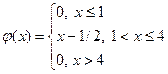 | 4) |  |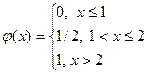
140. Укажите функцию, которая может быть интегральной функцией распределения некоторой случайной величины
| 1) | 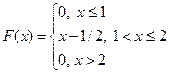 | 3) |  |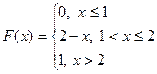
| 2) | 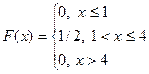 | 4) |  |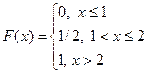
141. Случайная величина задана плотностью распределения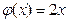 
в интервале (0; 1); вне этого интервала 
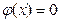. Вероятность 
равна …
142. Случайная величина задана плотностью распределения 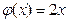в интервале (0; 1); вне этого интервала 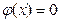. Математическое ожидание величины X равно …
| 1) | 1/2 | 2) | 1 | 3) | 4/3 | 4) | 2/3 |
143. Случайная величина задана плотностью распределения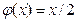 
в интервале (0; 2); вне этого интервала 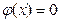. Математическое ожидание величины X равно …
| 1) | 1/2 | 2) | 1 | 3) | 4/3 | 4) | 2/3 |
144. Случайная величина задана плотностью распределения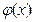 
в интервале (0; 1); вне этого интервала 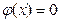. Математическое ожидание величины X равно …
| 1) | 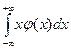 | 2) | 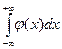 | 3) | 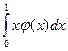 | 4) |  |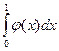
145. Дисперсия непрерывной случайной величины может быть рассчитана по формуле
| 1) | 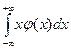| 2) | 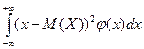 | 3) | 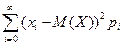 | 4) | |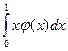
146. Непрерывная случайная величина равномерно распределена на отрезке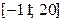 
. Вероятность 
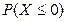равна …
| 1) | 11/32 | 2) | 5/16 | 3) | 10/31 | 4) | 11/31 |
147. Случайная величина Х распределена равномерно на отрезке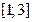 
. Тогда случайная величина 
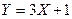имеет …
| 1) | нормальное распределение на отрезке  |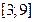
| 2) | нормальное распределение на отрезке  |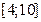
| 3) | другой (кроме равномерного и нормального) вид распределения |
| 4) | равномерное распределение на отрезке |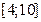
148. Непрерывная случайная величина равномерно распределена на отрезке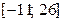 
. Вероятность 
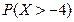равна …
| 1) | 29/38 | 2) | 29/37 | 3) | 30/37 | 4) | 15/19 |
149. Случайная величина Х распределена равномерно на отрезке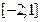 
. Тогда случайная величина 
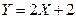имеет …
| 1) | нормальное распределение на отрезке  |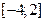
| 2) | равномерное распределение на отрезке  |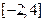
| 3) | нормальное распределение на отрезке |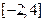
| 4) | другой (кроме равномерного и нормального) вид распределения |
150. Плотность вероятности равномерно распределенной непрерывной случайной величины имеет вид …
| 1) | 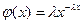 ,  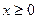| 2) |  ,  |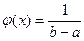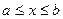
| 3) | 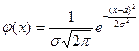 | 4) |  |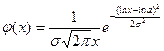
151. Случайная величина Х – равномерно распределена на отрезке [0; 15]. Математическое ожидание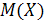 
равно …
152. Случайная величина Х – равномерно распределена на отрезке [0; 3]. Дисперсия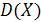 
равна …
| 1) | 0,75 | 2) | 1,5 | 3) | 3 | 4) | 6 |
153. Плотность вероятности нормально распределенной случайной величины имеет вид …
| 1) | 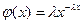, 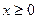| 2) | , |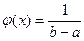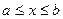
| 3) | 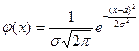| 4) | |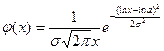
154. Плотность вероятности стандартной нормально распределенной случайной величины имеет вид …
| 1) | 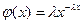, 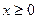| 2) | , |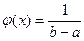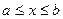
| 3) | 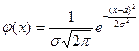| 4) |  |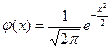
155. Плотность вероятности нормально распределенной случайной величины Х при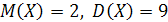 
, имеет вид:
| 1) | 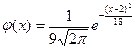 | 2) |  |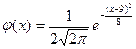
| 3) | 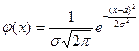| 4) |  |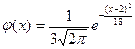
156. Нормально распределенная случайная величина Х задана плотностью 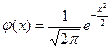. Дисперсия 
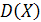равна …
157. Нормально распределенная случайная величина Х задана плотностью 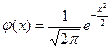. Математическое ожидание 
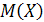равно …
158. Функция Лапласа имеет вид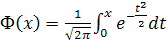 
. Укажите верные соотношения
| 1) | F(x) = – F(x) | 2) | F(– x) = – F(x) | 3) | F(– x) = F(x) | 4) | F(– x) = 0,5+F(x) |
159. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 15 и 5. Вероятность того, что в результате испытания Х примет значение из интервала (5; 20), равна
| 1) | F(20) – F(5) | 4) | F(2) – F(1) |
| 2) | F(20) + F(5) | 5) | F(1) – F(0) |
| 3) | F(1) + F(2) | 6) | F(5) + F(10) |
160. Значение интеграла от плотности распределения стандартной нормально распределенной величины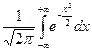 
равно…
161. Значение интеграла от плотности распределения стандартной нормально распределенной величины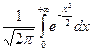 
равно…
