Функционального параметра

Пусть измерение z представляет собой аддитивную смесь истинного значения параметра y и погрешности измерений δ: z = y + δ.

Контролируемый параметр у описывается плотностью распределения f₁(у). Значения априорных вероятностей исправного и неисправного состояний рассчитываются по формулам:

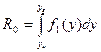; 1-R₀ = .

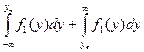Формулы для расчета вероятностей ложного и необнаруженного отказов имеют следующий вид:

Р_л.о = ;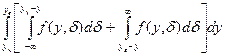

Р_н.о = ,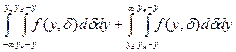

где 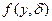— совместная плотность вероятностей контролируемого параметра у и погрешности измерений .

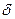При независимых параметре и ошибке измерения совместная плотность представляет собой произведение: f(y, 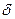) = f₁(y)f₂(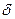) и формулы для Р_л.о и Р_н.о примут вид (рисунок 1):

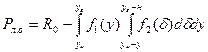(1)

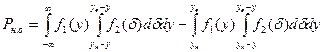. (2)

a) 6) в)

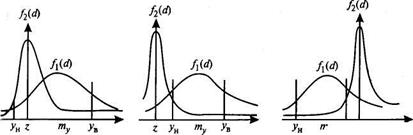
Рисунок 1 - Графики, поясняющие определение ошибок первого (а)

и второго (б, в) рода

В практике контроля систем ЛА наиболее часто принимается, что параметр у распределен по нормальному закону или по сильно усеченным законам, которые хорошо аппроксимируются равномер­ным распределением. Погрешности измерительных приборов в боль­шинстве случаев также распределены по нормальным законам, а по­грешности измерений, определяемые делениями шкалы отсчета, — но законам равной вероятности.

Рассмотрим три наиболее часто встречающихся случая возмож­ных сочетаний законов распределения контролируемого параметра у и ошибки измерения .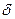

1.2 Первый случай.

Контролируемый параметр и ошибка измерения распределены по нормальному закону:

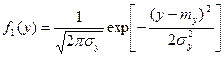; (3)

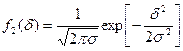, (4)

где m_y – математическое ожидание контролируемого параметра y;

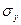- среднеквадратическое отклонение параметра y; 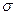- среднеквадратическое отклонение погрешности измерения .

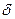Проведем замену переменных: 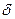/ 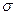= t; y – m_y / 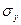= z. В этом случае формулы (1) и (2) с учетом (3) и (4) принимают вид:

Р_Л..О= Ф(к_В ) – Ф(к_Н )+ Р₁ ; (5)

Р_Н..О= Ф(к_В / 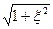) - Ф(к_Н / 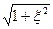) + Р₁ , (6)

где Ф(х) = 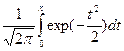-интегральная функция стандартного нормального распределения (функция Лапласа);

Р ₁= ;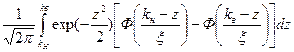

k_н=(y_н – m_y)/ 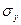; k_в= y_в – m_y / ; .

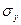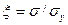Для симметричного относительно математического ожидания допуска

k_в = - k_н = k вероятности Р_Л..О и Р_Н..О определятся соотношениями:

Р_Л..О = 2Ф(k) – Р₂ ; (7)

Р_Н..О = 2Ф(k / 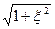) – Р₂, (8)

где Р₂ = 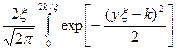Ф(z)dz.

Как следует из анализа приведенных выражений для вероятностей ложного и необнаруженного отказов, значения этих вероятностей полностью определяются шириной допуска k, значением априорной вероятности R₀, а также соотношением дисперсии погрешности измерений и дисперсии контролируемого параметра. Значение вероятности R₀ определяется требованиями к качеству функционирования систем и не может быть изменено. Следовательно, обеспечение приемлемых значений Р_{Л.. 0} и Р_{Н.. 0} может быть достигнуто путем подбора соответствующих средств измерений.

В случае, когда требования к точности оказываются нереализуемыми, обеспечение показателей достоверности контроля достигается либо проведением дублирующих измерений, либо введением контрольных допусков, отличных от эксплуатационных. При использовании дублирующих измерений в качестве результата измерения контролируемого параметра принимается его среднеарифметическое значение 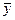= 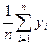, имеющее в п раз меньшую дисперсию, чем дисперсия средства измерения. Сужение контрольного допуска приводит к снижению вероятности необнаруженного отказа и увеличению вероятности ложного отказа, а его расширение — к увеличению Р_Н..0 и снижению Р_Л..О.

На рисунке 2 приведены номограммы зависимостей вероятностей Р_Л..О

и Р_{Н.. 0} от величины относительной ошибки измерения 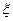для различных значений к. С помощью номограмм можно определить значе­ния ошибок первого и второго родов, если известны статистические характеристики контролируемого параметра и погрешности измере­ния, а также задан допуск на контрольный параметр. Номограммы позволяют решать и обратные задачи. Например, как обеспечить за­данную величину вероятностей ошибок Р_Л..0 и Р_{Н.. 0} при известном относительном допуске к.

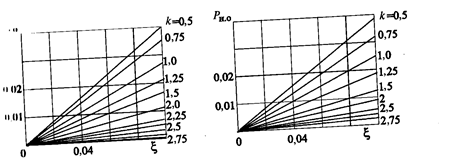
Рисунок 2 - Зависимости Р_Л..0 (а) и Р_Н..0 (б) от 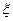для различных значений k при нормальном распределении у и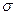

Пример. Пусть контрольный допуск равен к = у_в – m_y / σ_y =2σ_у / σ_y = 2 и необходимо, чтобы в процессе контроля вероятность Р_Н..0 не превысила 0,0031. Из номограммы следует, что эту задачу можно решить, подобрав соответствующим образом допустимую величину 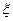, что соответствует выбо­ру аппаратуры контроля с соответствующими данному значению 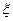точност­ными характеристиками. В данном случае относительная погрешность из­мерения 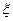не должна превышать 0,08.