Общие сведения. При расчетах установившихся режимов линейных электрических цепей синусоидального тока мгновенным значениям синусоидальных функций времени

При расчетах установившихся режимов линейных электрических цепей синусоидального тока мгновенным значениям синусоидальных функций времени, например, тока 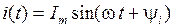, ставят в соответствие комплексное мгновенное значения .

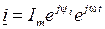Величины

;

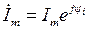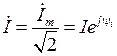
называют комплексными амплитудными и действующими значениями, соответственно. Аналогично для синусоидальных напряжений, э. д. с., электрических зарядов, магнитных потоков и т. д.

Для любого пассивного участка электрической цепи, содержащего элементы R, L и C, можно определить комплексное сопротивление

,

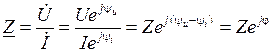
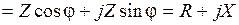и комплексную проводимость

.

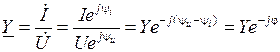
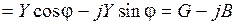Переход к комплексным действующим значениям напряжений и токов, комплексным сопротивлениям и проводимостям позволяет при расчетах использовать:

· уравнения, по форме совпадающие с законом Ома ;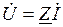

· 1-й закон Кирхгофа для любого узла схемы замещения цепи 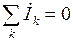(алгебраическая сумма по всем k ветвям узла);

· 2-й закон Кирхгофа для любого контура схемы замещения цепи: 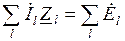(алгебраические суммы по всем l ветвям контура);

· методы расчета разветвленных цепей постоянного тока.

Мощности источников и пассивных участков цепи также представляются в комплексной форме:

,

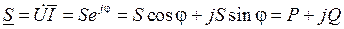где 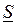– полная комплексная мощность; 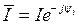– сопряженное комплексное действующее значение тока ().

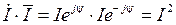В цепи синусоидального тока выполняется баланс комплексных, активных и реактивных мощностей источников и потребителей:

S _ист = S _пот ; Р _ист = Р _пот ; Q _ист = Q _пот .