Графа на основе упорядочения ребер графа

(алгоритм Прима-Краскала)

Такая задача возникает при прокладке дорог, газопроводов, линий электропередач и т.д., когда необходимо связать n точек так, чтобы общая длина «линий связи» была минимальной. Следует отметить, что «кратчайший остов графа» не имеет никакого отношения к дереву, дающему все кратчайшие пути, выходящие из некоторой выбранной вершины. Так, для графа (рис. 3.4), где числа, стоящие около ребер, являются их весами, дерево, дающее все кратчайшие пути, выходящие из вершины х₁, изображено на рис. 3.5, а кратчайший остов графа представлен на рис. 3.6.

X1

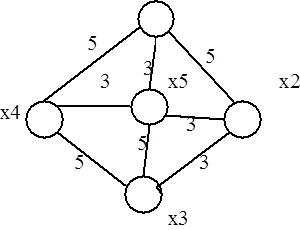
Рис. 3.4

X1

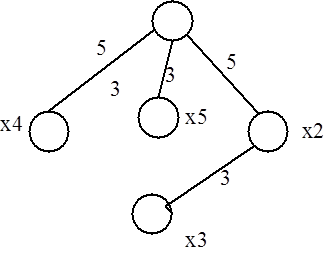
Рис. 3.5

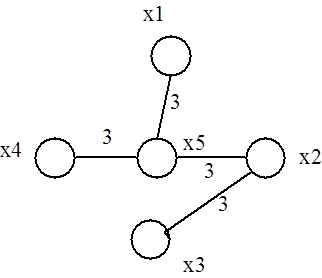
Рис. 3.6

Итак, кратчайший остов графа связывает кратчайшим образом все вершины графа, а не только х₁ с другими вершинами.

Для построения кратчайшего остова с помощью алгоритма, изложенного в п. 3.5.3, необходимо в п. 2 сформировать последовательность ребер в порядке возрастания их весов.