4.1 Производственная функция
Пусть 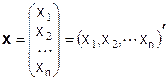 , х³0 – вектор затрат, т.е. хi – количество затрат i–го вида, i=1¸n. Связь между затратами и выпуском называется производственной функцией q = f(x) = f(x1, x2,... xn)
, х³0 – вектор затрат, т.е. хi – количество затрат i–го вида, i=1¸n. Связь между затратами и выпуском называется производственной функцией q = f(x) = f(x1, x2,... xn)
где q – максимально возможный выпуск единственного вида продукции при заданном векторе затрат.
Мы предполагаем, что производственная функция удовлетворяет двум требованиям (аксиомам):
1.Существует такое подмножество пространства затрат, которое называется экономической областью, в котором увеличение любого вида затрат не приводит к уменьшению выпуска х1 ³ х2 Þ f(x1) ³ f(x2), что эквивалентно требованию неотрицательности первых частных производных производственной функции по всем переменным 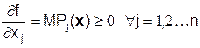
2.Существует выпуклое [2] подмножество экономической области R, называемое особой областью, в которой матрица Гессе производственной функции 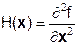 отрицательно определена " x ÎR.
отрицательно определена " x ÎR.
В особой области R подмножества, ограниченные линиями уровня производственной функции { x ÎR:f(x)³q0} (т.н. производственные множества), выпуклы для любого q0.
В области R также справедливо 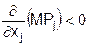 , т.е. вторые «чистые» частные производные производственной функции по любому фактору затрат (по любой из переменных xj) отрицательны. Это соотношение называется законом убывающей отдачи, оно означает, что по достижению определенного уровня увеличение затрат данного типа приводит к снижению их эффективности, т.е. уменьшению предельного продукта. Отметим, что вдоль изокванты df = 0, то (MP d x) = 0, и если из всех переменных изменяются только две xj и xk, то MPj dxj + MPk dxk = 0. При этих предположениях вдоль изокванты на плоскости (xj, xk)
, т.е. вторые «чистые» частные производные производственной функции по любому фактору затрат (по любой из переменных xj) отрицательны. Это соотношение называется законом убывающей отдачи, оно означает, что по достижению определенного уровня увеличение затрат данного типа приводит к снижению их эффективности, т.е. уменьшению предельного продукта. Отметим, что вдоль изокванты df = 0, то (MP d x) = 0, и если из всех переменных изменяются только две xj и xk, то MPj dxj + MPk dxk = 0. При этих предположениях вдоль изокванты на плоскости (xj, xk) 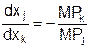 т.е. в экономической области наклон изоквант всегда отрицателен, поскольку все MPj положительны.
т.е. в экономической области наклон изоквант всегда отрицателен, поскольку все MPj положительны.
Основными характеристиками производственной функции, кроме предельных продуктов, являются отдача от расширения масштаба производства и возможности замещения. Отдача от увеличения масштаба характеризует поведение производственной функции при том условии, что все затраты возрастают в одинаковой пропорции, т.е. она характеризуется соотношением между f(x) и f(a x).[3] Мы говорим, что эффективность не зависит от масштаба производства (отдача постоянна), если производственная функция однородная степени 1, т.е. f(a x) = af(x). Производственная функция характеризуется возрастающей (убывающей) отдачей, если f(a x) > (<) a f(x).
4.2 Геометрические представления
Рассмотрим геометрическую иллюстрацию для случая двух переменных x1 и x2.
На рис.9 изображены две изокванты: f(x)=q1 и f(x)=q2, (q1>q2). Границы особой области показаны жирным пунктиром. Внутри особой области предельные продукты MP1 и MP2 положительны, а наклоны изоквант отрицательны; вне особой области один из предельных продуктов становится отрицательным, что означает уменьшение выпуска при росте затрат одного из факторов. Граница 1 формируется из точек, в которых MP1 равен нулю, а граница 2 – из точек, в которых MP2 равен нулю. Соответственно, в точках пересечения изоквант с границей 1 касательные к изоквантам горизонтальны, а в точках пересечения с границей 2 касательные к изоквантам вертикальны. Границу 1 также можно интерпретировать как линию минимальных затрат фактора 2, необходимых для заданного объема выпуска (вся изокванта f(x)=q1 лежит выше точки а). Аналогично, граница 2 есть линия минимальных затрат фактора 1, необходимых для заданного объема выпуска (вся изокванта f(x)=q1 лежит правее точки b). Чем больше выпуск q, тем дальше расположена соответствующая изокванта от начала координат (тем больше затраты); в случае производственной функции постоянной отдачи изокванты получаются одна из другой пропорциональным растяжением вдоль лучей, исходящих из начала (изокванты гомотетичны).
3.5 Неоклассическая теория фирмы
Эта теория построена на таких предположениях:
1. Целью фирмы является максимизация прибыли: P = R–C, где R – доход, а С – издержки
2. Фирма производит продукцию только одного вида.
3. Фирма действует в условиях совершенной конкуренции, т.е. цена выпуска р и цены факторов производства wj заданы и не зависят от деятельности фирмы.
При сделанных предположениях доход и издержки соответственно равны:
R=pq = p f(x) C = 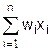 = (w x) (51)
= (w x) (51)
Математически эта задача формулируется следующим образом:
P(x) = R–C = p f(x) – (w x) ® max при условиях: х³0 (52)
Если предположить, что затраты всех видов реально сделаны, то получим, что в точке оптимума стоимость предельных продуктов равна плате за ресурсы. Это означает, что оптимальное распределение трат таково, что при увеличении затрат j–го вида на единицу доход от увеличения выпуска в точности равен цене единицы j–го ресурса, т.е. затратам. Одновременное пропорциональное изменение всех цен не влияет на оптимальный размер выпуска.
 Проиллюстрируем полученные результаты геометрически для случая двух факторов производства. Изобразим на рисунке изокванты – линии постоянного объема выпуска, и изокосты – линии фиксированных денежных затрат. В двухфакторной задаче изокосты есть лини уровня функции С = x1w1 + x2w2, где С – положительная константа, и представляют собой семейство параллельных прямых. При заданном уровне издержек С величина оптимального выпуска соответствует той из изоквант, которая касается выбранной изокосты (по Лагранжу линии уровня целевой функции и функции ограничений имеют в точке оптимума общую касательную).
Проиллюстрируем полученные результаты геометрически для случая двух факторов производства. Изобразим на рисунке изокванты – линии постоянного объема выпуска, и изокосты – линии фиксированных денежных затрат. В двухфакторной задаче изокосты есть лини уровня функции С = x1w1 + x2w2, где С – положительная константа, и представляют собой семейство параллельных прямых. При заданном уровне издержек С величина оптимального выпуска соответствует той из изоквант, которая касается выбранной изокосты (по Лагранжу линии уровня целевой функции и функции ограничений имеют в точке оптимума общую касательную).
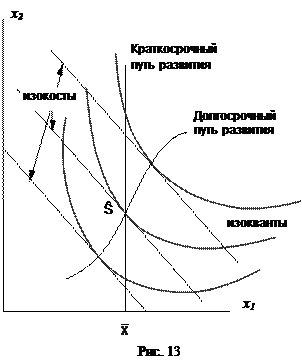
Совокупность точек, в которых изокванты касаются изокост можно рассматривать с двух точек зрения. С первой точки зрения эта кривая представляет на плоскости (x1,x2) оптимальное распределение затрат для каждого заданного объема выпуска при отсутствии иных ограничений на затраты, кроме требования их положительности. Такая кривая на плоскости (x1,x2) называется кривой долгосрочного развития. Как ранее отмечалось, развитие называется краткосрочным, если на затраты факторов производства наложены дополнительные ограничения, связанные, например, с необходимостью выполнения уже заключенных договоров. На рис. 13 линия краткосрочного развития вертикальна и отвечает ограничению 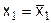 . Линии долго- и краткосрочного развития пересекаются в единственной точке
. Линии долго- и краткосрочного развития пересекаются в единственной точке 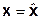 . Только в этой точке структура затрат краткосрочной линии развития оптимальна.
. Только в этой точке структура затрат краткосрочной линии развития оптимальна.
[1] Отличить вектор-градиент от обычной частной производной можно по тому признаку, что у градиента переменная, по которой дифференцируют, это вектор x, и, значит, она выделена жирным шрифтом.
[2] Множество называется выпуклым, если любые две его точки можно соединить прямой, целиком принадлежащей этому множеству.
[3] Геометрически это означает, что мы исследуем поведение производственной функции при движении вдоль луча, порожденного вектором x.
 2015-05-22
2015-05-22 299
299







