3.1. Экстремумы в многомерных задачах
Пусть 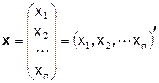 n-мерный вектор, а F(x) – дважды непрерывно дифференцируемая функция переменной x, т.е. F(x) функция n переменных xi. Обозначим градиент[1] F(x) в точке x 0
n-мерный вектор, а F(x) – дважды непрерывно дифференцируемая функция переменной x, т.е. F(x) функция n переменных xi. Обозначим градиент[1] F(x) в точке x 0 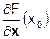 =
= 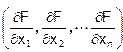
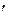 т.е. это n-мерный вектор-столбец, координатами которого являются частные производные F(x) по координатам xi, вычисленные в некоторой точке x 0. Как известно, первый дифференциал представляется в виде скалярного произведения вектора-градиента
т.е. это n-мерный вектор-столбец, координатами которого являются частные производные F(x) по координатам xi, вычисленные в некоторой точке x 0. Как известно, первый дифференциал представляется в виде скалярного произведения вектора-градиента 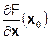 на вектор смещения d x.
на вектор смещения d x.
dF(x 0) = 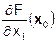 dx1 +
dx1 + 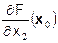 dx2 + …+
dx2 + …+ 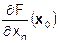 dxn = (
dxn = ( 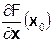 d x)
d x)
3.1.2 Матрица Гессе (гессиан)
Для того, чтобы в векторной форме записать второй дифференциал нам понадобится построить специальную матрицу. Вычислив градиенты каждой из координат вектора-градиента 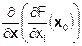 , мы получим n векторов, каждый из которых содержит n координат, равных вторым частным производным функции F(x). Расположив координаты этих n векторов по столбцам матрицы, мы получим квадратную n-мерную матрицу; такая матрица называется матрицей Гессе или гессианом функции F(x):
, мы получим n векторов, каждый из которых содержит n координат, равных вторым частным производным функции F(x). Расположив координаты этих n векторов по столбцам матрицы, мы получим квадратную n-мерную матрицу; такая матрица называется матрицей Гессе или гессианом функции F(x):
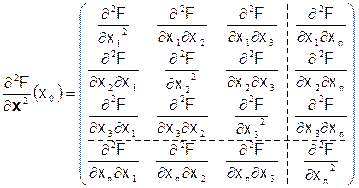
Т.к. 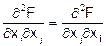 , то гессиан всегда симметричная матрица, и, следовательно, может порождать квадратичную форму. Второй дифференциал d2F представляет собой сумму произведений вторых частных производных на произведение соответствующих приращений независимых переменных:
, то гессиан всегда симметричная матрица, и, следовательно, может порождать квадратичную форму. Второй дифференциал d2F представляет собой сумму произведений вторых частных производных на произведение соответствующих приращений независимых переменных:
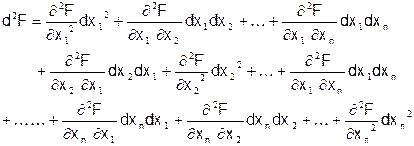
Легко видеть, что перед нами квадратичная форма относительно приращений переменных dx1, dx2, dx3, … dxn, коэффициенты которой совпадают с элементами матрицы Гессе (гессиана). d2F(x 0) = ( d x¢ 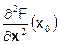 d x)
d x)
Здесь d x¢ =(dх1, dх2, dх3,... dхn) – вектор-строка, а d x – соответствующий вектор-столбец, круглые скобки означают скалярное (матричное) произведение. При введенных обозначениях выражение для приращения дважды непрерывно дифференцируемой функции двух переменных выглядит абсолютно так же, как и для приращения функции одной переменной и может рассматриваться как приращение функции одной векторной переменной
DF=F(x0 +D x)– F(x0)= 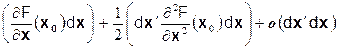
3.1.3 Необходимые и достаточные условия экстремума
Вполне аналогично случаю одной переменной необходимым условием экстремума является тождественное равенство нулю первого дифференциала, что эквивалентно требованию равенства градиента нуль-вектору 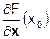 = 0. Точки, в которых это условие выполнено, называются, как и в случае одной переменной, стационарными.
= 0. Точки, в которых это условие выполнено, называются, как и в случае одной переменной, стационарными.
Достаточное условие наличия экстремума формулируется так же, как и в случае одной переменной: для наличия экстремума в стационарной точке достаточна знакоопределенность второго дифференциала, причем положительная определенность достаточна для минимума, а отрицательная определенность - для максимума:
d2F(x 0) = ( d x¢ 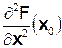 d x) > 0 Û min
d x) > 0 Û min
d2F(x 0) = ( d x¢ 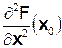 d x) < 0 Û max
d x) < 0 Û max
По критерию Сильвестра для положительной определенности квадратичной формы необходимо и достаточно, чтобы все главные миноры матрицы квадратичной формы были положительны, а для отрицательной определенности квадратичной формы необходимо и достаточно, чтобы знаки главных миноров чередовались, т.е. чтобы у минора i-го порядка был знак (–1)i. Таким образом, критерий Сильвестра, примененный к гессиану, дает нам инструмент для выяснения вопроса о наличии экстремума в стационарной точке функции нескольких переменных.
3.2 Классическая задача математического программирования. Метод множителей Лагранжа (случай двух переменных)
3.2.1 Постановка задачи и функция Лагранжа
Пусть нужно найти max F(x1,x2) при условии g(x1,x2) = b. Функция F(x1,x2) называется целевой функцией, а линия g(x1,x2) = b - линией ограничений, точки, в которых условие g(x1,x2) = b выполнено, называются допустимыми.
Введем в рассмотрение новую функцию L: L(x1,x2,y) = F(x1,x2) + y (b – g(x1,x2))
Функция L зависит от вектора x и скалярного множителя y; переменную y называют множителем Лагранжа, а функцию L(x1,x2,y) – функцией Лагранжа. Стационарные точки функции Лагранжа имеют следующие особенности:
1. Любая стационарная точка функции Лагранжа принадлежит допустимому множеству, т.к. 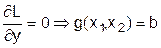 ;
;
2. Поскольку 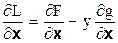 , то во всякой стационарной точке функции Лагранжа градиенты целевой функции и функции ограничений пропорциональны (
, то во всякой стационарной точке функции Лагранжа градиенты целевой функции и функции ограничений пропорциональны (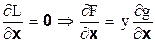 )
)
3.2.2 Необходимые условия экстремума в классической задаче математического программирования (задаче Лагранжа)
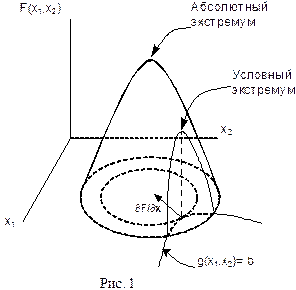 Т.к. производная по направлению всегда равна проекции градиента на это направление, необходимым условием экстремума является равенство нулю проекции градиента целевой функции на допустимое множество (градиент должен быть перпендикулярен касательной к кривой ограничений). Из приведенных свойств стационарных точек функции Лагранжа следует
Т.к. производная по направлению всегда равна проекции градиента на это направление, необходимым условием экстремума является равенство нулю проекции градиента целевой функции на допустимое множество (градиент должен быть перпендикулярен касательной к кривой ограничений). Из приведенных свойств стационарных точек функции Лагранжа следует
1. В стационарной точке функции Лагранжа линия уровня целевой функции касается линии допустимых значений g(x1,x2) = b.
2. В стационарной точке функции Лагранжа градиент целевой функции перпендикулярен кривой ограничений потому что:
- он параллелен градиенту g(x1,x2)
- градиент g(x1,x2) перпендикулярен линии g(x1,x2) = b как своей линии уровня
- вектор, параллельный перпендикуляру к линии, сам к ней перпендикулярен
Поэтому в стационарной точке функции Лагранжа градиент целевой функции имеет нулевую проекцию на допустимое множество: линию g(x1,x2) = b
Таким образом необходимым условием наличия экстремума у функции F(x1,x2) при условии g(x1,x2) = b является стационарность функции L(x1,x2,y)
Другими словами, стационарные точки функции F(x1,x2) на множестве допустимых значений совпадают со стационарными точками функции L(x1,x2,y).
3.2 Задача нелинейного программирования
3.2.1 Постановка задачи
Задача нелинейного программирования формулируется следующим образом: найти максимум целевой функции n переменных, при том условии, что их значения подчинены m ограничениям-неравенствам и требованию неотрицательности F(x1, x2,... xn) ® max
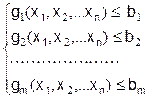
x1 ³0, x2 ³0,.... xn ³0,
В векторной форме эту же задачу запишем следующим образом
F(x) ® max g (x) £ b х³0
Здесь g (x) m–мерная вектор-функция, а b –m-мерный вектор.
Легко видеть, что сформулированная задача является аналогом стандартной задачи линейного программирования, с тем отличием, что целевая функция и ограничения представлены нелинейными выражениями
3.2 Задача с ограничениями неотрицательности
Рассмотрим частный случай задачи, когда из всех ограничений на инструментальные переменные наложено только требование неотрицательности
F(x) ® max х³0
т.е. мы ищем максимум целевой функции в первом (неотрицательном) ортанте. Если максимум (локальный или глобальный) находится во внутренней точке x0 допустимого множества (ортанта), то необходимым условием первого порядка является равенство нулю градиента: 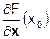 = 0. Вместе с последним условием в точке максимума, естественно, выполнено и условие (
= 0. Вместе с последним условием в точке максимума, естественно, выполнено и условие ( 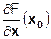 x0) = 0.
x0) = 0.
Если точка максимума x0 находится на границе допустимой области, то это означает, что одна или более координат точки равны нулю. Пусть, например, число переменных равно трем и в точке максимума х=0, т.е. максимум достигается на плоскости YZ. На этой плоскости ограничение х≥0 активно (превратилось в равенство), мы находимся в ситуации задачи Лагранжа, и необходимым условием экстремума становится перпендикулярность градиента допустимому множеству. Значит единственной ненулевой координатой градиента становится х-координата. При этом если мы ищем именно максимум, то обязательно 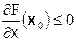 , т.к. иначе функция будет расти от плоскости YZ вправо, и максимум по х окажется при х >0, а мы предположили, что максимум по х на границе при х=0. Следовательно, градиент целевой функции в точке максимума перпендикулярен линии ограничения х=0 и смотрит наружу. Значит, и в случае расположения максимума на границе справедливо условие: скалярное произведение вектора-градиента на координаты точки, в которой градиент вычислен, равно нулю (
, т.к. иначе функция будет расти от плоскости YZ вправо, и максимум по х окажется при х >0, а мы предположили, что максимум по х на границе при х=0. Следовательно, градиент целевой функции в точке максимума перпендикулярен линии ограничения х=0 и смотрит наружу. Значит, и в случае расположения максимума на границе справедливо условие: скалярное произведение вектора-градиента на координаты точки, в которой градиент вычислен, равно нулю ( 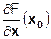 x0) = 0 причем для всех координат справедливо
x0) = 0 причем для всех координат справедливо 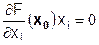 . Т.е. в точке максимума либо координата хi равна нулю, либо производная по этой координате равна 0. Имеем компактную запись необходимого условия максимума при ограничениях неотрицательности как одновременное выполнение одного векторного неравенства и одного векторного равенства:
. Т.е. в точке максимума либо координата хi равна нулю, либо производная по этой координате равна 0. Имеем компактную запись необходимого условия максимума при ограничениях неотрицательности как одновременное выполнение одного векторного неравенства и одного векторного равенства:
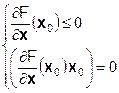
 2015-05-22
2015-05-22 730
730








