2015-05-22
294
Работоспособность алгоритма, рассмотренного в п. 5, проверялась на тестовых задачах ZDT3, ZDT6, DTLZ4 из стандартного набора тестов для непрерывных многокритериальных задач [0] – см. Табл. 1. При решении всех тестовых задач использовались следующие значения параметров алгоритма:
параметр разделения σshare=0.01;
доля отбираемых для скрещивания индивидов Tr=0.3;
параметр рекомбинации CrossoverRate=0.7;
мутационный параметр MutationRate=1.0;
число индивидов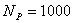 
;
число поколений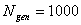 
.
Табл. 1. Тестовые задачи.
| Задача | Частные критерии оптимальности | Размерность и множество допустимых значений D |
| ZDT3 |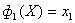 
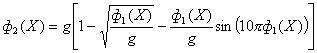
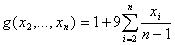
| n =30
|
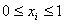
| ZDT6 |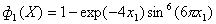 
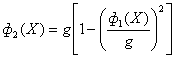
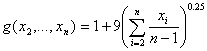
| n =10
|
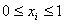
| DTLZ4 |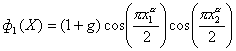 
 , 
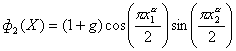
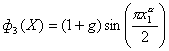
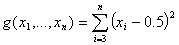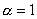
| n =12
|
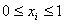
Рис. 2 - 4, иллюстрирующие результаты тестирования, получены с помощью свободно распространяемой утилиты gnuplot. На рисунках представлены точные фронты Парето (сплошные линии) и их аппроксимации, полученные с помощью программной системы PRADIS//FRONT (обозначены крестиками). Количество поколений, при которых получены приведенные на рисунках результаты, изменяется от примерно 300 до 1000.
Результаты тестирования показывают, что используемый в системе алгоритм приближенного построения множества Парето позволяет получить хорошие решения для тестовых задач ZDT3, ZDT6 и удовлетворительные результаты – для задачи DTLZ4.
