2015-05-22
1895
Дополнениеммножества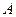 
до универсального множества 
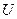называется множество 
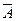, элементы которого не принадлежат .
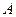Пересечениемдвух множеств А и В называется множество A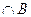 
, состоящее изэлементов, принадлежащих множеству А и множеству В.
Объединением множеств А и В называется множество A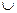 
B, состоящее изэлементов, принадлежащих множеству А или множеству В.
Разностьюмежду множествами А и В называется множество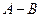 
, состоящее изэлементов множества А, которые не принадлежат множеству В.
Симметрической разностьюмножеств А и В называется множество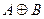 
(
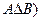, равное объединению двух разносте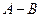й и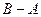 
.
Порядок выполнения операций в выражениях определяется следующим образом. Прежде всего выполняется операция дополнения множества до универсального множества 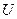. Затем выполняются последовательно слева направо действия, заданные в скобках. Пересечение считают теоретико-множественным умножением, а объединение – теоретико-множественным сложением. Поэтому сначала выполняют операцию пересечения и только после нее – объединения или разности. Пересечение и объединение рассматривают как умножение и сложение в силу того, что своими свойствами они напоминают эти арифметические операции. По этой же причине пустое множество 
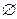похоже на число 0, а универсальное множество 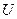– на число 1.
|
|
|
Законы теории множеств, верные для любых множеств А, В, С.
1. A Ç B = B Ç A – закон коммутативности пересечения.
2. A È B = B È A – закон коммутативности объединения.
3. A Ç(B Ç C) = (A Ç B)Ç C – закон ассоциативности пересечения.
4. A È(B È C) = (A È B)È C – закон ассоциативности объединения.
5. A Ç(B È C) = (A Ç B)È(A Ç C)– закон дистрибутивности пересечения относительно объединения.
6. A È(B Ç C) = (A È B)Ç(A È C) – закон дистрибутивности объединения относительно пересечения.
7. A Ç A = A – закон идемпотентности пересечения.
8. A È A = A – закон идемпотентности объединения.
9. A ÇÆ = Æ. 10. A ÈÆ= A. 11. A Ç 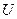= A. 12. A È = .
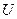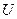13. A Ç 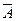=Æ – закон противоречия. 14. A È 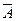= 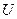– закон исключенного третьего.
15. 
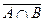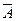= È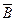 
– закон де Моргана для дополнения пересечения.
16. 
= 
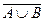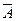
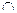
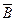– закон де Моргана для дополнения объединения.
17. A Ç(B È A) = A – закон поглощения. 18. A È(B Ç A) = A – закон поглощения.
19. (A Ç B)È(A Ç 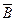) = A – закон склеивания. 20. (A È B)Ç(A È 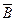) = A – закон склеивания.
21. A =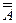 
– закон инволюции. 22. A - B = A Ç 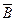. 23. A Å B = (A È B) -(A Ç B).
Замечание 1. Очевидно, что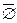 
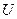= и 
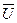= Æ.
Замечание 2. Законы де Моргана можно распространить на большее число
множеств.
Пример 1. Задано универсальное множество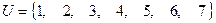 
, множества 
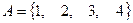и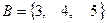 
. Выполнить действия 
, 
, , , 
, , , 
, 
, 
, 
.
|
|
|
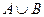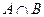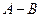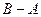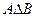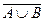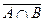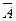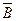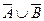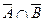Решение. Выполним действия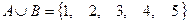 
, 
, 
, 
, =(
, 
, 
, 
, = 
, = 
.
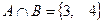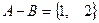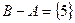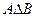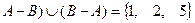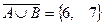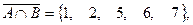
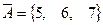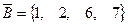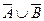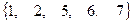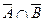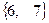Пример 2. Задано универсальное множество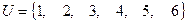 
, множества 
, 
, 
, 
, 
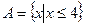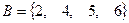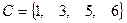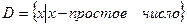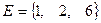. Найти множество 
.
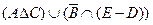Решение. Зададим множества 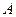и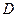 
перечислением элементов 
, 
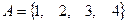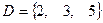. Выполним последовательно действия: 
, 
, 
, 
, 
.
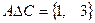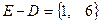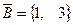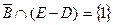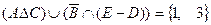Пример 3. Доказать справедливость утверждения A Å(B - A Ç B) = A È B с помощью таблицы принадлежности и используя законы теории множеств.
Решение.
Составим таблицу принадлежности, рассмотрев четыре возможных случая принадлежности некоторого элемента двум множествам:
| A | B | A Ç B | B - A Ç B | A Å(B - A Ç B) | A È B |
| - | - | - | - | - | - |
| - | + | - | + | + | + |
| + | - | - | - | + | + |
| + | + | + | - | + | + |
Результаты выполнения действий над множествами в левой и правой частях совпадают, значит, утверждение справедливо.
Применим законы логики.
Возьмем левую часть A Å(B - A Ç B) данного равенства и сведем ее к правой части A È B.
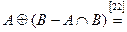
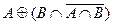
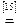
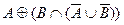
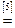
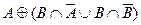
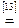
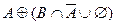
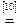
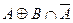
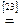
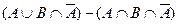
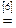
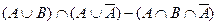
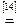
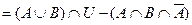
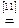
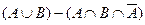
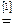
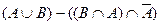
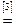
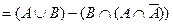
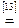
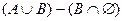
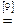
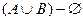
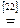
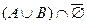
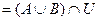
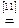
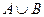. Утверждение справедливо.
