А = {1, 2, 3}, тогда сочетания из 3 элементов по 2 – это наборы (1, 2), (1, 3), (2, 3). Всего 3 набора, при этом надо помнить, что (1, 2) = (2, 1) и т.п., так как при образовании сочетаний порядок элементов не учитывается.
Определение 41. Число сочетаний, которые можно образовывать, выбирая различными способами m элементов из n,обозначают 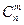 и называют биномиальными коэффициентами (они совпадают с биномиальными коэффициентами формулы бинома Ньютона для степени n).
и называют биномиальными коэффициентами (они совпадают с биномиальными коэффициентами формулы бинома Ньютона для степени n).
Теорема 6. Число различных выборок объема m из совокупности 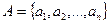 объема n, если выбор производится без возвращения и без учета порядка выбираемых элементов, то есть число сочетаний, равно
объема n, если выбор производится без возвращения и без учета порядка выбираемых элементов, то есть число сочетаний, равно 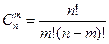 .
.
Свойства сочетаний:
1) 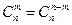 , 2)
, 2) 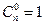 , 3)
, 3) 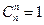 , 4)
, 4) 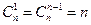 , 5)
, 5) 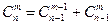 , 6)
, 6) 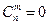 , если m > n.
, если m > n.
В приведенном выше примере 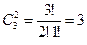 . (3 набора)
. (3 набора)
 2015-05-22
2015-05-22 642
642








