Поиск наибольшей монотонно возрастающей подпоследовательности

Рассмотрим вначале более простую формулировку задачи: требуется найти длину наибольшей монотонно возрастающей подпоследовательности (а не саму подпоследовательность).

Алгоритм 1: перебор подпоследовательностей

Пусть задана упорядоченная последовательность чисел: A = <a₀, a₁,..., a_n-1>. Подпоследовательностью из А называют последовательность, которую можно получить из А путем удаления из нее некоторого множества элементов. Задача состоит в том, чтобы найти длину наибольшей монотонно возрастающей подпоследовательности, которая содержится в А.

Самая простая идея состоит в том, чтобы алгоритм решения задачи построить на основе полного перебора всех подпоследовательностей.

Реализация

Любую подпоследовательность из А можно представить, указав множество номеров элементов последовательности А, включаемых в подпоследовательность. Создадим массив q[n] и присвоим его элементам значения 0,1,2,..., n-1. Будем считать эти числа множеством и будем перебирать все подмножества из него. Для каждого подмножества будем проверять монотонность соответствующей подпоследовательности и фиксировать ее длину.

Для перебора всех подмножеств из множества q можно использовать следующую функцию из syst.h:

int subsetnext(int n, int r, int* q)

Здесь r – размер выбираемого подмножества. Функция возвращает номер очередного подмножества. Если все подмножества уже исчерпаны, функция возврашает 0.

Оценка эффективности алгоритма

Общее количество подпоследовательностей будет равно числу всех подмножеств из n-элементного множества. Это число равно 2ⁿ. Если с - это наибольшее время, которое требуется для проверки одной подпоследовательности, то для времени работы нашего алгоритма будем иметь:

.

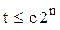Время работы алгоритма в среднем равно:

t = Const×2ⁿ_.

Результаты испытания алгоритма.

Исходная последовательность - случайные числа из интервала [0, 999]. Длина исходной последовательности: 150 000. Время выполнения: ¥.

Алгоритм 2: метод рейтинга

Рассмотрим более эффективный алгоритм, который реализует так называемый метод рейтинга. Пусть

A = <a₁, a₂,..., a_n >

исходная последовательность. Свяжем с каждым элементом последовательности a_i целое число - рейтинг p_i. Всем рейтингам вначале присвоим единичные значения. Рассмотрим следующую процедуру:

for i: =1 to n-1

for j: = i+1 tо n

if a_j > a_i and p_j < p_i+1 then p_j : = p_i+1

Можно убедиться, что после выполнения последней процедуры наибольший из рейтингов будет равен искомой величине - длине наибольшей монотонно возрастающей последовательности. Ниже показано состояние массива рейтингов p для каждого шага i процедуры (1). Длина исходной последовательности - 10, исходная последовательность A = < 7, 3, 5, 4, 8, 0, 5, 6, 2, 9 >.

| ------------------------------------

| 7 3 5 4 8 0 5 6 2 9

| ------------------------------------

1 | 1 1 1 1 2 1 1 1 1 2

2 | 1 1 2 2 2 1 2 2 1 2

3 | 1 1 2 2 3 1 2 3 1 3

4 | 1 1 2 2 3 1 3 3 1 3

5 | 1 1 2 2 3 1 3 3 1 4

6 | 1 1 2 2 3 1 3 3 2 4

7 | 1 1 2 2 3 1 3 4 2 4

8 | 1 1 2 2 3 1 3 4 2 5

9 | 1 1 2 2 3 1 3 4 2 5

10 | 1 1 2 2 3 1 3 4 2 5

В первой строке указан исходный массив, в левой колонке - номер шага. Красным цветом отмечены элементы массива рейтингов, подвергаемых проверке на текущем шаге. Решением задачи является число L = 5.

Ниже приведена реализация алгоритма решения задачи в виде функции С++.

int subs2(int N, int* x)

{ int i,k,L=1;

int* p= new int[N];

for (i=0;i<N;i++) p[i]=1;

for (i=0;i<N;i++)

for (k=i+1;k<N;k++)

{ if (x[k]>x[i] && p[i]+1>p[k]) p[k]=p[i]+1;

if (p[k]>L) L=p[k];

}

delete[] p;

return L;

}

Результаты испытания алгоритма.

Исходная последовательность - случайные числа из интервала [0, 999]. Длина исходной последовательности: 150 000. Найденная длина наибольшей монотонно возрастающей подпоследовательности: 624. Время выполнения: 73.3 c.

Асимптотический класс функции сложности для метода рейтингов:

F_t(n) = O(n²).

Алгоритм 3: быстрый (Робинсона-Шенстеда (Robinson-Schensted algorithm))

В этом алгоритме последовательно формируется вспомогательная последовательность m, длина которой равна длине обнаруженной подпоследовательности, а элемент последовательности m_i говорит о том, что существует монотонная подпоследовательность, в которой элемент исходной последовательности, равный m_i занимает позицию номер i.

int subs3(int N, int* b)

{ int i, j, L = 0;

int* m = new int[N];

for (i = 0; i < N; i++) m[i] = 0;

m[0] = b[0];

for (i = 1; i < N; i++)

{ if (b[i] > m[L]) m[++L] = b[i];

else for(j = 0; j <= L; j++) if (b[i] < m[j]) { m[j] = b[i]; break; }

}

delete[] m;

return L + 1;

}

Отметим следующее. Вспомогательная последовательность m является монотонно возрастающей по построению. Для выполнения поиска элемента m_i для его замены при невыполнении условия b[i]>m[L] можно использовать метод бинарного поиска. Именно в этом случае и получаем F(n) = c×n×ln(n).

Результаты испытания алгоритма.

Тестирование быстрого алгоритма выполнялось при таких же условиях, как и для метода рейтингов. Время выполнения алгоритма равно 0.05 с. Асимптотический класс функции сложности:

F_t(n) = O(n×ln(n)).

Результаты испытания алгоритма.

Тестирование быстрого алгоритма выполнялось при таких же условиях, как и для метода рейтингов. Время выполнения алгоритма равно 0.05 с.

Ниже в таблице показано преобразование рабочего массива m по шагам для исходной последовательности A = < 7, 3, 5, 4, 8, 0, 5, 6, 2, 9 >.