2015-05-22
1620
Задача 4. (Математика ЕГЭ-2015. 30 вариантов +800 задач. Вариант 19)
31 декабря 2014 года Евгений взял в банке 1 млн. рублей в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся часть долга (т.е. увеличивает долг на а%), Затем Евгений переводит в банк очередной транш. Евгений выплатил кредит за два транша, переведя в первый раз 540 тыс. рублей, а во второй 649,6 тыс. рублей. Под какой процент банк выдал кредит Евгению?
Решение: Отличие данной задачи от предыдущих задач заключается в том, что в формуле выплаты кредита за второй год присутствуют два различных значения транша, т.е. Х 1 и Х 2:
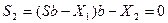Или: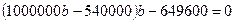 
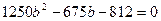
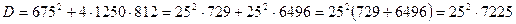
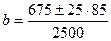. Т.к. банковский коэффициент не может быть отрицательным, то:
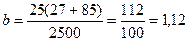а = 12%
Ответ: 12 %
Задача 5. (Математика ЕГЭ-2015. 30 вариантов +800 задач. Вариант 1)
1 января 2015 года Александр Сергеевич взял в банке 1,1 млн. рублей в кредит. Схема выплаты кредита следующая – 1 числа каждого следующего месяца банк начисляет 1% на оставшуюся сумму долга (то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платеж. На какое минимальное количество месяцев Александр Сергеевич может взять кредит, чтобы ежемесячные выплаты были не более 275 тыс.рублей?
Решение: Пусть сумма взятого кредита S, ставка по кредиту a %, а коэффициент увеличения ставки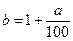 
. Тогда долг через месяц составит S b. После погашения части долга Х, остаток кредите составит: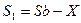 
Через два месяца: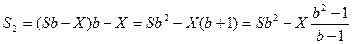 
Через 3 месяца: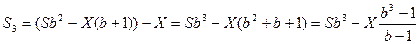 
Через 4 месяца: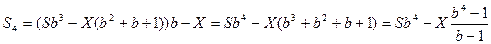 
Т.о. через n месяцев: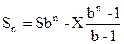 
.
Подставляя данные, получаем следующее выражение:
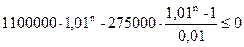
Ноль в правой части формулы означает, что весь кредит будет погашен. Из данного неравенства выразим выражение, содержащее степень:
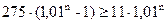
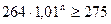, откуда: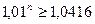 
Используем формулу для приближенного вычисления значений, близких к единице: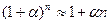 
, 
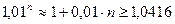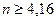. Т.к. 
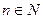, то n = 5
