Для универсального множества 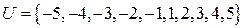 , множества
, множества 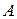 , заданного списком и множества
, заданного списком и множества 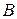 , состоящего из множества корней уравнения, заданного в варианте,
, состоящего из множества корней уравнения, заданного в варианте,
а) найти множества: 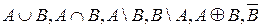 ;
;
б) найти 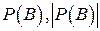 .
.
1. 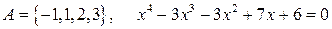
2. 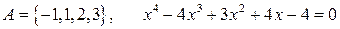
3. 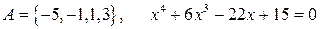
4. 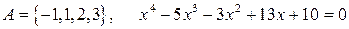
5. 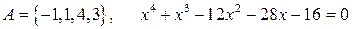
6. 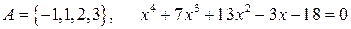
7. 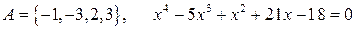
8. 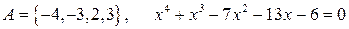
9. 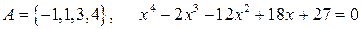
10. 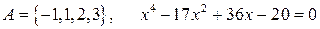
11. 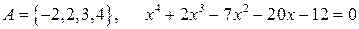
12. 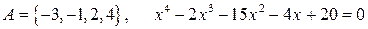
13. 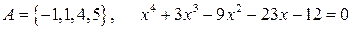
14. 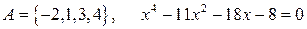
15. 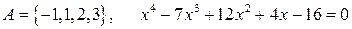
16. 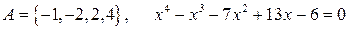
17. 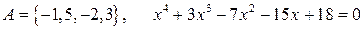
18. 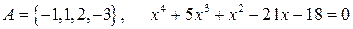
19. 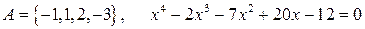
20. 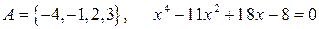
Задание 2.5.
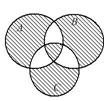
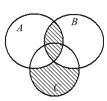
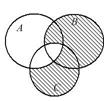
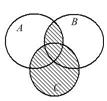
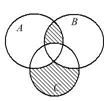
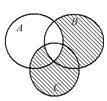
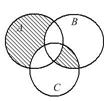
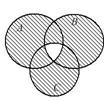
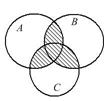
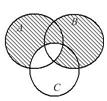
Выразить с помощью символов множество, заштрихованное на диаграммах Эйлера.
1. 
| 2. 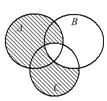
|
3. 
| 4. 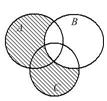
|
5. 
| 6. 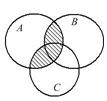
|
7. 
| 8. 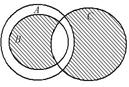
|
9. 
| 10. 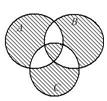
|
11. 
| 12. 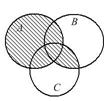
|
13. 
| 14. 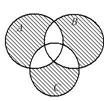
|
15. 
| 16. 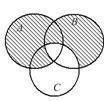
|
17. 
| 18. 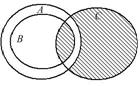
|
19. 
| 20. 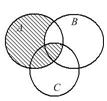
|
Задание 2.6.
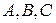 -множества, координаты которых удовлетворяют условиям 1, 2, 3 соответственно. Изобразите в системе координат
-множества, координаты которых удовлетворяют условиям 1, 2, 3 соответственно. Изобразите в системе координат 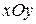 множество
множество 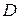 , полученное из множеств
, полученное из множеств 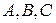 по заданной формуле.
по заданной формуле.
1. 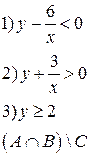
| 2. 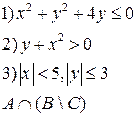
|
3. 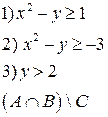
| 4. 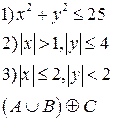
|
5.  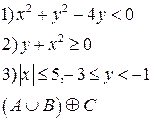
| 6. 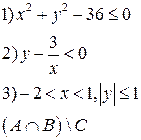
|
7. 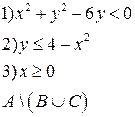
| 8. 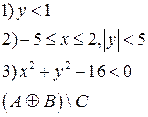
|
9. 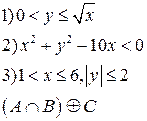
| 10. 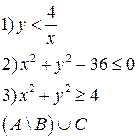
|
11. 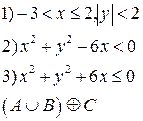
| 12. 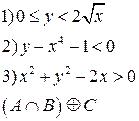
|
13. 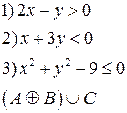
| 14. 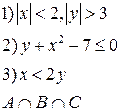
|
15. 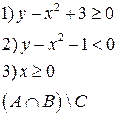
| 16. 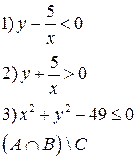
|
17. 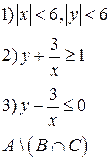
| 18. 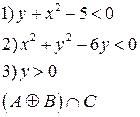
|
19. 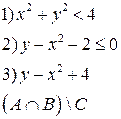
| 20. 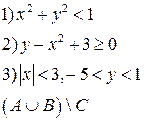
|
Задание 2.7.
Решить систему соотношений относительно множеств 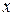 и указать условия совместности системы.
и указать условия совместности системы.
| № | Система | № | Система | № | Система |
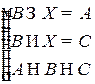
| 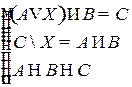
| 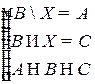
| |||
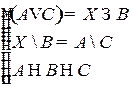
| 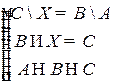
| 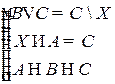
| |||
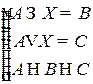
| 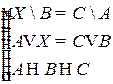
| 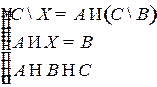
| |||
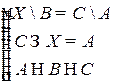
| 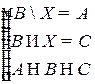
| 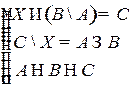
| |||
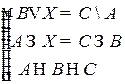
| 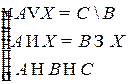
| 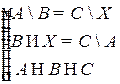
| |||
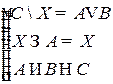
| 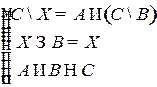
| 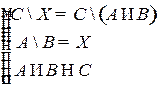
| |||
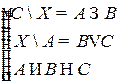
| 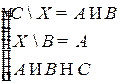
| 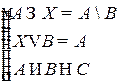
|
 2015-05-22
2015-05-22 279
279








