Удар тела о неподвижную преграду

Рассмотрим тело (шар) массой М, ударяющееся о неподвижную плиту. Действующей на тело ударной силой будет при этом реакция плиты; импульс этой силы за время удара назовем 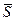. Пусть нормаль к поверхности тела в точке его касания с плитой проходит через центр масс тела (для шара это будет всегда). Такой удар тела называется центральным. Если скорость 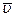центра масс тела в начале удара направлена по нормали 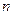к плите, то удар будет прямым,

в противном случае — косым.

1. Случай прямого удара. Составляя в этом случае уравнение (154) в проекции на нормаль 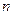(см. рис. 375) и учитывая, что 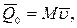а 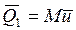получим

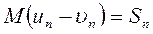
Но при прямом ударе 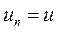, , 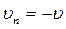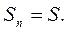Следовательно,

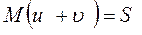
Второе уравнение, необходимое для решения задачи, дает равенство (156)

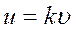
Из полученных уравнений, зная М, 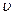, k, найдем неизвестные величины 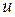и S. При этом

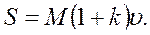
Как видим, ударный импульс будет тем больше, чем больше коэффициент восстановления k. На эту зависимость S от k и было указано в § 153.

Чтобы определить среднюю величину ударной силы (реакции), надо дополнительно знать время удара т, которое можно найти экспериментально.

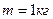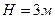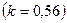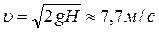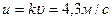Пример. При падении стального шара массой с высоты на стальную плиту получим и . Ударный импульс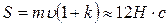

Если время удара 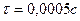, то средняя величина ударной реакции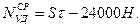

2. Случай косого удара Пусть в этом случае скорость 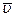центра масс тела в начале удара образует с нормалью к плите угол 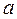, а скорость 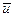в конце удара — угол 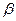(рис. 377).

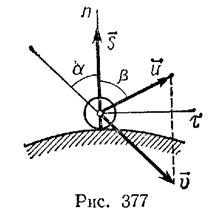
Тогда уравнение (154) в проекциях па касательную 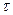и нормаль 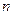даст

,

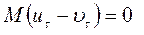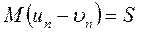
Коэффициент восстановления в данном случае равен отношению модуле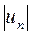й и 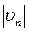, так как удар происходит только но направлению нормали к поверхности (влиянием трения пренебрегаем) Тогда с учетом знаков проекций получим 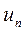—— 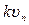. В результате окончательно находим.

, , .

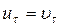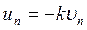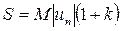Из полученных уравнений можно найти модуль и направление скорости в конце удара и ударный импульс, если величины М, 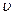, 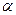и k известны. В частности, из первого равенства, замечая, что 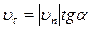и 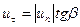, получаем

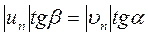
Откуда

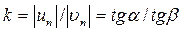
Следовательно, при косом ударе отношение тангенса угла падения к тангенсу угла отражения равно коэффициенту восстановления. Так как 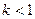, то 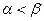т. е. угол падения всегда меньше угла отражения.