Геометрическим образом (графиком) функции двух независимых переменных 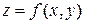 в пространстве R3 является некоторая поверхность Q. Выберем на ней точку
в пространстве R3 является некоторая поверхность Q. Выберем на ней точку  .
.
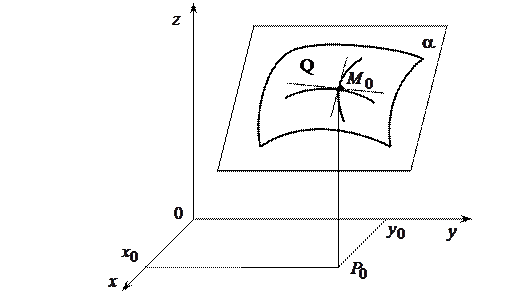
Определение. Касательной плоскостью к поверхности Q в данной точке 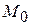 называется плоскость, которая содержит все касательные к кривым, проведенным на поверхности через эту точку.
называется плоскость, которая содержит все касательные к кривым, проведенным на поверхности через эту точку.
Уравнение касательной плоскости к поверхности 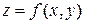 в точке
в точке 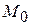 имеет вид
имеет вид
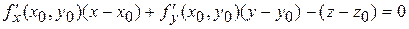 .
.
Если уравнение поверхности Q задано неявной функцией
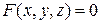 , то:
, то:
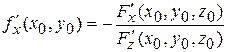 ,
, 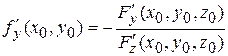 .
.
Подставим значения частных производных в уравнение касательной:
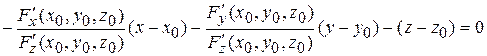 .
.
Следовательно, уравнение касательной плоскости к поверхности 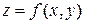 в точке
в точке 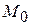 в случае неявного задания функции имеет вид
в случае неявного задания функции имеет вид
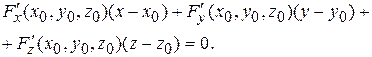
Определение. Точка, в которой 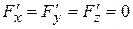 или хотя бы одна из этих производных не существует, называется особой точкой поверхности. В такой точке поверхность может не иметь касательной.
или хотя бы одна из этих производных не существует, называется особой точкой поверхности. В такой точке поверхность может не иметь касательной.
Определение. Нормалью к поверхности Q в данной точке  называется прямая, проходящая через эту точку перпендикулярно к касательной плоскости, проведенной в данной точке поверхности.
называется прямая, проходящая через эту точку перпендикулярно к касательной плоскости, проведенной в данной точке поверхности.
Запишем уравнения нормали к поверхности 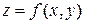 в точке
в точке  , пользуясь условием перпендикулярности прямой и плоскости:
, пользуясь условием перпендикулярности прямой и плоскости:
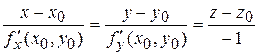
Если поверхность Q задана неявно функцией 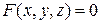 то уравнения нормали принимают вид
то уравнения нормали принимают вид
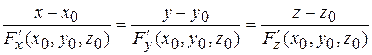 .
.
Пример. Найти уравнения касательной плоскости и нормали к поверхности 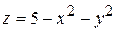 в точке
в точке 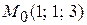 .
.
Решение. Уравнение поверхности задано явной функцией. Вычислим частные производные функции в точке 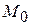 :
:
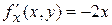 ,
, 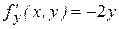 ,
,
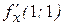
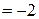 ,
, 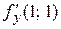
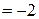 .
.
Тогда уравнение касательной плоскости примет вид

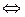
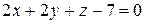 .
.
Найдем уравнения нормали:

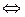
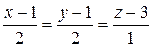
Пример. Найти уравнение касательной плоскости и нормали к поверхности 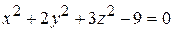 в точке
в точке 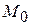
 .
.
Решение. Уравнение поверхности задано неявно. Вычислим частные производные функции в точке 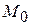
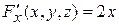 ,
, 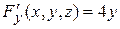 ,
, 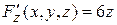 ,
,
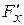

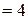 ,
, 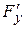

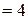 ,
, 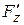

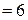 .
.
Следовательно, уравнение касательной плоскости имеет вид
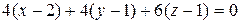
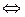
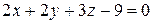 .
.
Находим уравнения нормали
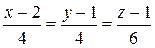
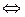
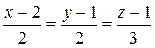 .
.
 2014-02-04
2014-02-04 18373
18373
