Из рассуждений, приведенных в § 153, следует, что при неупругом ударе происходит потеря кинетической энергии соударяющихся тел. Наибольшей эта потеря будет при абсолютно неупругом ударе. Подсчитаем, какую кинетическую энергию теряет система при абсолютно неупругом ударе двух тел.
Считая, что соударяющиеся тела движутся поступательно, и обозначая их общую скорость после абсолютно неупругого удара через и, получим для кинетической энергии системы в начале и в конце удара значения:
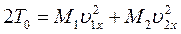 ,
, 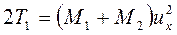 (162)
(162)
Потерянная при ударе кинетическая энергия равна 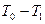 . Представим эту разность в виде
. Представим эту разность в виде
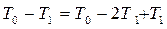 (163)
(163)
Так как из формулы (160) следует, что
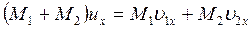
То отсюда
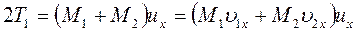 (164)
(164)
Подставляя в правую часть равенства (163) вместо Т0 и Т1 их значения из формул (162), а вместо 2Т1— правую часть выражения (164), получим:
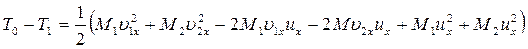
Или
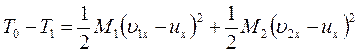 (165)
(165)
Разности (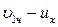 ) и (
) и (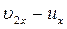 ) показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся тел. Их можно назвать потерянными при ударе скоростями. Тогда из формулы (165) вытекает следующая теорема Кар но *: кинетическая энергия, потерянная системой тел при абсолютно неупругом ударе, равна той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями.
) показывают, насколько уменьшилась при ударе скорость каждого из соударяющихся тел. Их можно назвать потерянными при ударе скоростями. Тогда из формулы (165) вытекает следующая теорема Кар но *: кинетическая энергия, потерянная системой тел при абсолютно неупругом ударе, равна той кинетической энергии, которую имела бы система, если бы ее тела двигались с потерянными скоростями.
Если удар не является абсолютно неупругим (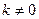 ), то аналогичными преобразованиями можно найти, что кинетическая энергия, потерянная при ударе двух тел, определяется равенством
), то аналогичными преобразованиями можно найти, что кинетическая энергия, потерянная при ударе двух тел, определяется равенством
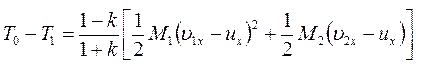 (165’)
(165’)
Рассмотрим частный случай абсолютно неупругого удара по первоначально неподзижногау телу. В этом случае 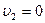 и
и
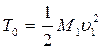 ,
, 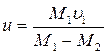
Тогда
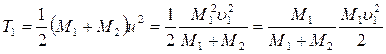
Или
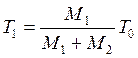 (166)
(166)
Формула (166) показывает, какая энергия остается у системы после удара. Отметим два интересных предельных случая.
1.Масса ударяющего тела много больше массы ударяемого (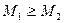 ) В этом случае можно считать М1+М2
) В этом случае можно считать М1+М2 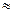 M1 и формула (166) дает
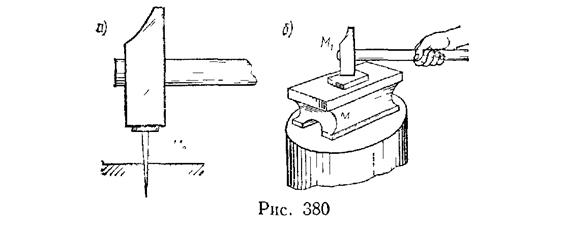
M1 и формула (166) дает 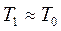 . Следовательно, хотя удар и является абсолютно непругим, потеря кинетической энергии при ударе почти не происходит, и система после удара начнет двигаться почти с той же кинетической энергией, которая у нее была в начале удара. На практике такой результат нужно, очевидно, получать при забивании гвоздей, свай и т п. Следовательно, в этом случае нужно, чтобы масса молотка была намного больше массы гвоздя (рис. 380, а).
. Следовательно, хотя удар и является абсолютно непругим, потеря кинетической энергии при ударе почти не происходит, и система после удара начнет двигаться почти с той же кинетической энергией, которая у нее была в начале удара. На практике такой результат нужно, очевидно, получать при забивании гвоздей, свай и т п. Следовательно, в этом случае нужно, чтобы масса молотка была намного больше массы гвоздя (рис. 380, а).
2. Масса ударяемого тела много больше массы ударяющего (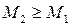 ) В этом случае можно считать М1/(М1+М2)
) В этом случае можно считать М1/(М1+М2) 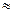 0, и формула (166) дает
0, и формула (166) дает 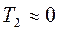 . Таким образом, здесь при ударе почти вся кинетическая энергия расходуется на деформацию соударяющихся тел, по окончании удара тела можно считать неподвижными.
. Таким образом, здесь при ударе почти вся кинетическая энергия расходуется на деформацию соударяющихся тел, по окончании удара тела можно считать неподвижными.
Практически такой результат нужно, очевидно, получать при ковке, клепке и т. п. Следовательно, в этих случаях нужно, чтобы масса поковки вместе с наковальней (или масса заклепки вместе с поддержкой) была много больше массы молота (рис. 380, б).
§ 157*. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА
Рассмотрим тело, имеющее ось вращения z (рис. 381).
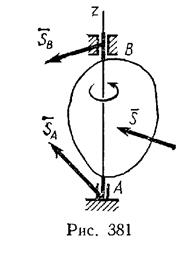
Пусть в некоторый момент времени к телу будет приложен ударный импульс 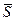 . Тогда по уравнению (155')
. Тогда по уравнению (155')
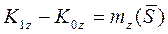
так как моменты относительно оси z импульсивных реакций 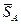 и
и 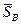 возникающих в подшипниках, будут равны нулю.
возникающих в подшипниках, будут равны нулю.
Условимся обозначать угловую скорость тела в начале удара через 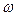 , а в конце удара — через
, а в конце удара — через 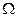 . Тогда
. Тогда 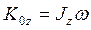 ,
, 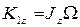 , и окончательно получим:
, и окончательно получим:
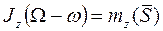 или
или 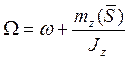 (167)
(167)
Формула (167) определяет изменение угловой скорости тела при ударе. Из нее следует, что угловая скорость тела за время удара изменяется на величину, равную отношению момента ударного импульса к моменту инерции тела относительно оси вращения.
Задача 187. Колесо 1, вращающееся с угловой скоростью 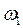 , ударяет выступом D1 о выступ D2 первоначально неподвижного колеса 2 (рис. 382).
, ударяет выступом D1 о выступ D2 первоначально неподвижного колеса 2 (рис. 382). 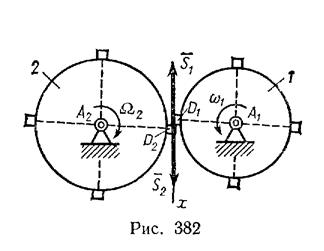
Радиусы колес и их моменты инерции относительно осей 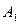 и
и 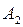 соответственно равны
соответственно равны 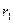 ,
, 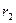 ,
, 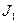 ,
, 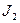 Определить угловую скорость
Определить угловую скорость 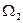 колеса 2 в конце удара, если коэффициент восстановления при ударе равен k.
колеса 2 в конце удара, если коэффициент восстановления при ударе равен k.
Решение. При ударе на колеса действуют численно равные ударные импульсы 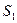 и
и 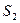 , (
, (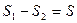 ). Тогда, составив уравнение (167) для каждого из колес и учтя, что
). Тогда, составив уравнение (167) для каждого из колес и учтя, что 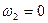 , получим:
, получим:
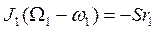 ,
, 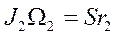
Исключив из этих уравнений S, придем к равенству
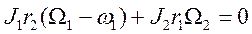 (а)
(а)
Так как скорости точек D1, и D2 в начале и в конце удара равгы соответственно 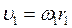 ,
, 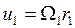 ,
, 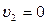 ,
, 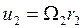 , то формула (156'), определяющая коэффициент восстановления при прямом ударе, даст
, то формула (156'), определяющая коэффициент восстановления при прямом ударе, даст
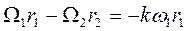 (б)
(б)
Исключив из уравнений (а) и (б) 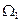 найдем окончательно
найдем окончательно
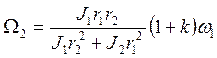
Импульсивные реакции. Найдем, чему равны при ударе импульсивные реакции подпятника А и подшипника В. Проведем оси Ахуz так, чтобы центр масс С тела лежал в плоскости Ауz (рис. 383, а). Изобразим искомые импульсивные реакции их составляющими вдоль этих осей. Пусть АВ = b, а расстояние точки С от оси Az равно а. Составим уравнения (154') в проекциях на все три оси, а уравнения (155') в проекциях на оси Ах и Ау (уравнение в проекции на ось Az уже использовано при получении равенства 167). Поскольку тело за время удара не перемещается, векторы 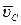 и
и 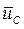 будут параллельны оси Ах; следовательно,
будут параллельны оси Ах; следовательно, 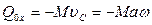 ,
, 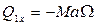 ,
, 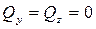 . Используя одновременно при составлении уравнений (155') формулы (34) из § 115, получим
. Используя одновременно при составлении уравнений (155') формулы (34) из § 115, получим
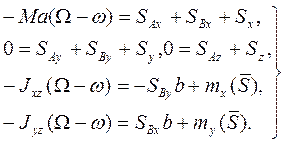 (168)
(168)
Уравнения (168) и служат для определения неизвестных импульсивных реакций 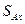 ,
, 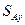 ,
, 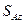 ,
, 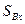 ,
, 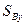 . Входящая сюда разность
. Входящая сюда разность 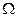 —
— 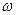 находится из равенства (167).
находится из равенства (167).
Центр удара. Появление при ударе импульсивных реакций нежелательно, так как может привести к ускорению износа или даже к разрушению частей конструкции (подшипников, вала и т. п.). Найдем, можно ли произвести удар по телу, закрепленному на оси, так, чтобы импульсивные реакции в подшипниках А и В вообще не возникли. Для этого найдем, при каких условиях можно удовлетворить уравнениям (168), положив в них 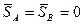 . Если
. Если 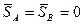 , то 2-е и 3-е из уравнений (168) примут вид: Sy=0, Sz=0. Чтобы удовлетворить этим уравнениям, надо направить импульс S перпендикулярно плоскости Ауz, т. е. (по принятому условию) плоскости, проходящей через ось вращения и центр масс тела. Допустим, что импульс S имеет такое направление (рис. 383, б). Поскольку при
, то 2-е и 3-е из уравнений (168) примут вид: Sy=0, Sz=0. Чтобы удовлетворить этим уравнениям, надо направить импульс S перпендикулярно плоскости Ауz, т. е. (по принятому условию) плоскости, проходящей через ось вращения и центр масс тела. Допустим, что импульс S имеет такое направление (рис. 383, б). Поскольку при
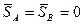 вид системы (168) не зависит от выбора на оси Az начала координат, проведем для упрощения дальнейших расчетов плоскость Оху так, чтобы импульс S лежал в этой плоскости. Тогда
вид системы (168) не зависит от выбора на оси Az начала координат, проведем для упрощения дальнейших расчетов плоскость Оху так, чтобы импульс S лежал в этой плоскости. Тогда 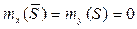 и последние два уравнения системы (168) при
и последние два уравнения системы (168) при 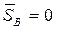 дадут
дадут 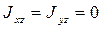 . Это означает (см. § 104), что плоскость Оху, п которой лежит импульс S, должна проходить через такую точку О, для которой ось г является главной осью инерции тела; в частности, как показано в § 104, условия
. Это означает (см. § 104), что плоскость Оху, п которой лежит импульс S, должна проходить через такую точку О, для которой ось г является главной осью инерции тела; в частности, как показано в § 104, условия 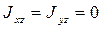 будут выполняться, если плоскость Оху является для тела плоскостью симметрии. Обратимся, наконец, к 1-му из уравнении (168). Поскольку
будут выполняться, если плоскость Оху является для тела плоскостью симметрии. Обратимся, наконец, к 1-му из уравнении (168). Поскольку 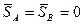 и
и 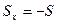 (см. рис 383, б), оно принимает_вид M a (
(см. рис 383, б), оно принимает_вид M a (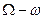 )=S. Одновременно уравнение (167), так как в нашем случае
)=S. Одновременно уравнение (167), так как в нашем случае 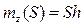 , дает
, дает 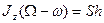 . Исключая из двух полученных равенств разность
. Исключая из двух полученных равенств разность 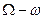 , находим.
, находим.
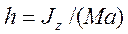 (169)
(169)
Формула (169) определяет, па каком расстоянии h от оси г должен быть приложен ударный импульс.
Итак, для того чтобы при ударе по телу, закрепленному на оси z, в точках закрепления этой оси не возникло импульсивных реакций, надо:
1)чтобы ударный импульс был расположен в плоскости Оху, перпендикулярной
оси г и проходящей через такую точку О тела, для которой ось г является главной
осью инерции (в частности, плоскость Оzу может быть плоскостью симметрии чела);
2)чтобы удар был направлен перпендикулярно плоскости, проходящей через
ось вращения г и центр месс С тела;
3)чтобы ударный импульс был приложен на расстоянии 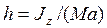 от оси (поту сторону от оси, где находится центр масс).
от оси (поту сторону от оси, где находится центр масс).
Точка К, через которую при этом будет проходить ударный импульс, не вызывающий ударных реакций в точках закрепления оси, называется центром удара.
3aметим, что согласно формуле (169) центр удара совпадает с центром качаний физического маятника. Следовательно, как было показано в § 129, h>а, т. е. расстояние ст оси до центра удара больше, чем до центра масс. Если ось вращения
проходит через центр масс тела, то а=0. и \;ы получаем h = 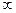 В этом случае центра удара на конечном расстоянии не существует, и любой удар по телу будет пере-
В этом случае центра удара на конечном расстоянии не существует, и любой удар по телу будет пере-
даваться на ось.
Приложения полученных результатов иллюстрируются следующими примерами.
1. При конструировании вращающегося курка (см задачу 189) или маятникового копра (прибор в виде маятника для испытания материалов на удар) и т. п. надо
ось вращения располагать так, чтобы точка тела, производящая }дар, была по от-
ношению к этой оси центром удара.
2.При работе ручным молотом его надо брать за рукоятку в таком месте, чтобы точка, которой производится удар, была относительно руки центром удара. В противном случае руку будет «обжигать».
3.При ударе палкой, чтобы не «обжечь» руку (рис. 384), надо ударять тем местом, которое по отношению к руке будет центром удара. Если палку считать однородным длиной l а ось вращения совпадающей с его концом, то тогда 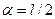 ,
, 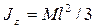 и
и 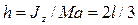 .
.
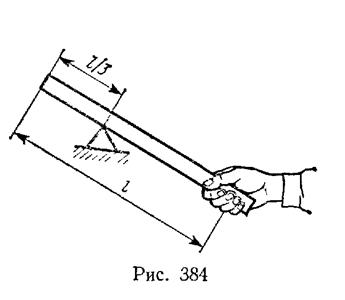
Следовательно, (рис. 384) удар надо производить тем местом стержня, которое находится на расстоянии 2 l /3 от руки или l /3 от другого конца стержня.
Задача 188. Мишень представляет собой тонкую однородную пластину, которая может вращаться вокруг оси Аz (рис. 385).
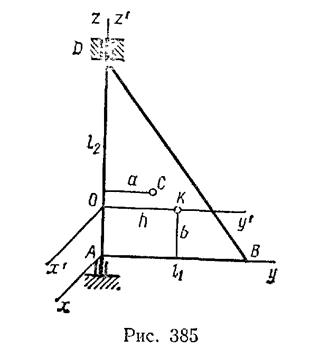
Форма мишени — прямоугольный треугольник ABD с катетами AB= l 1 AD= l 2. Определить, где у мишени находится центр удара, если известно, что для пластины ABD осевой момент инерции 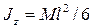 , а центробежный —
, а центробежный — 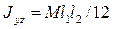 (M —масса пластины, оси Ауz в плоскости пластины).
(M —масса пластины, оси Ауz в плоскости пластины).
Решение. Так как у треугольной пластины ABD центр тяжести С находится на расстоянии 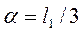 от оси Аz, то по формуле (169) расстояние центра удара К от той же оси будет
от оси Аz, то по формуле (169) расстояние центра удара К от той же оси будет 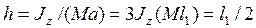 .
.
Остается определить, на каком расстоянии Ь находится центр удара от оси Ау. Для этого надо найти на оси Аz точку О, для которой эта ось будет главной. Если через точку О провести оси Ох'у'z ', параллельные осям Ахуz, то точка О будет главной, когда 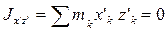 и
и 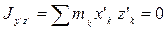
Первое условие, очевидно, всегда выполняется, так как для пластины все 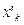 =0. Чтобы найти, когда выполняется второе условие, воспользуемся тем, что нам известно значение
=0. Чтобы найти, когда выполняется второе условие, воспользуемся тем, что нам известно значение 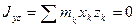 и что
и что 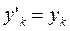 ,а
,а 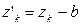 .Тогда
.Тогда 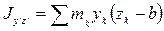 =
= 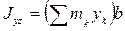 =
= 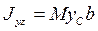 , где
, где 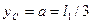 . Следовательно
. Следовательно 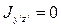 если
если 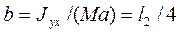 .
.
Итак, центр удара находится в точке К с координатами 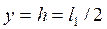 ,
, 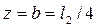 .
.
Задача 189. Вращающийся курок AD в момент начала удара по ударнику В (рис. 386) имеет угловую скорость 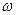 .
.
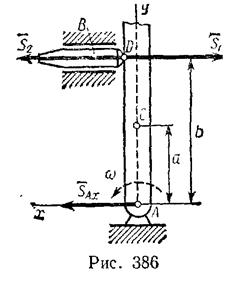
Определить скорость ударника в конце удара и импульсивное давление на ось А. Массы М и m курка и ударника, момент инерции 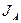 курка относительно оси А, коэффициент восстановления k и расстояния а и b известны (точка С — центр масс курка).
курка относительно оси А, коэффициент восстановления k и расстояния а и b известны (точка С — центр масс курка).
Решение. Обозначим ударные импульсы, действующие на курок и ударник при ударе через S1 и S2. Тогда для курка [по уравнению (167)] и для ударника [по уравнению (154')], учитывая, что S1=S2=S, a 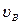 =0, получим:
=0, получим:
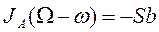 ,
, 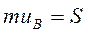 (a)
(a)
У момента Sb взят знак минус, так как момент направлен противоположно направлению вращения курка. Кроме того, поскольку для точки D курка 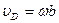 , a
, a 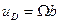 (
(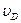 —скорость в начале удара,
—скорость в начале удара, 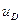 — в конце), то формула (158'), определяющая коэффициент восстановления при прямом ударе двух тел, дает:
— в конце), то формула (158'), определяющая коэффициент восстановления при прямом ударе двух тел, дает:
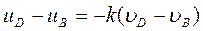 или
или 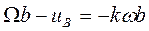 .
.
Подставляя сюда 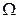 и S т уравнений (а), найдем скорость ударника в конце удара;
и S т уравнений (а), найдем скорость ударника в конце удара;
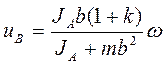
Для определения 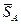 — импульсивной реакции, действующей со стороны оси на курок, составляем для курка уравнение (154) в проекциях на оси Ах и Ау. Учитывая, что
— импульсивной реакции, действующей со стороны оси на курок, составляем для курка уравнение (154) в проекциях на оси Ах и Ау. Учитывая, что 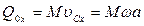 ,
, 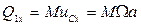 , найдем:
, найдем:
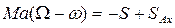 ,
, 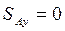 (б)
(б)
Но из уравнений) (a) 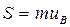 ,
, 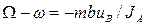 . Подставляя эти величины
. Подставляя эти величины
в равенство (б) и заменяя из его значением, получим окончательно
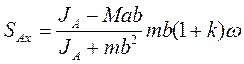
При 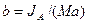 точка D является центром удара и
точка D является центром удара и 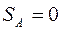 .
.
 2015-06-10
2015-06-10 3864
3864
