Плотность распределения вероятностей f(x) характеризует вероятность попадания случайной величины в некоторый интервал. Эта вероятность равна
площади, заключенной между осью абсцисс и функцией f(x) на интервале 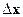
(Рис.8). Функция f(x) = 
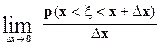 .
.
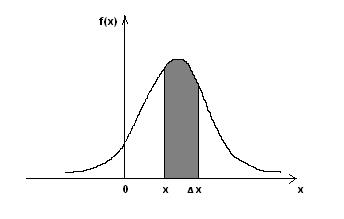
Рис. 8
Плотность распределения обладает следующими свойствами:
1. f (x) ≥ 0
2. 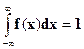
3. p(a 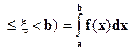
4. f(x) = 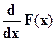 в точках непрерывности функции f(x).
в точках непрерывности функции f(x).
Понятие функции распределения, математического ожидания и дисперсии имеет такой же смысл, как в дискретном случае, а вычисляются соответственно по формулам (6) – (8).
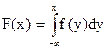 (6)
(6)
M (x) = 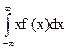 (7)
(7)
D ( x) = 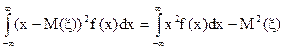 (8)
(8)
Пример 13. Случайная величина x распределена по закону, определяемому плотностью распределения вероятностей вида
f (x) = 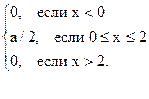

Найти параметр a, F(x), M (x), D ( x).
Параметр a найдем из свойства 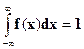 , интеграл
, интеграл 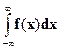 разобьем на сумму трех интегралов
разобьем на сумму трех интегралов
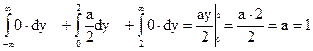
Нарисуем график плотности распределения f (x) (Рис.9)
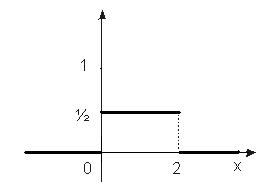
Рис. 9
Вычислим функцию распределения, для этого рассмотрим интервалы 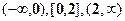 .
.
1. х Î (- ∞, 0) 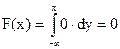 ,
,
2. х Î [0, 2] 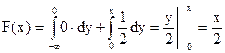 ,
,
3. х  (2,
(2,  )
) 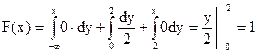 .
.
График функции приведен на Рис. 10.
Вычислим математическое ожидание и дисперсию:

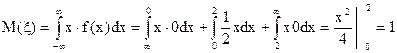
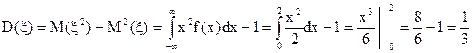
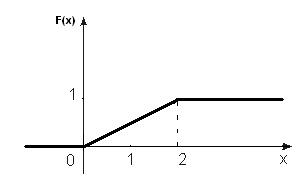
Рис.10
 2015-06-10
2015-06-10 527
527








