1. Равномерное распределение.  Случайная величина x непрерывного типа называется распределенной равномерно на отрезке [a,b], если ее плотность распределения постоянна на этом отрезке:
Случайная величина x непрерывного типа называется распределенной равномерно на отрезке [a,b], если ее плотность распределения постоянна на этом отрезке:
f(x) = 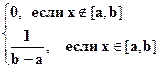 (9)
(9)
Вычислим математическое ожидание и дисперсию: 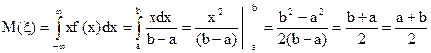 ,
,
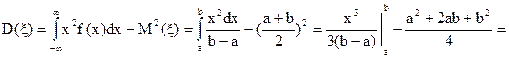

= 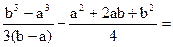
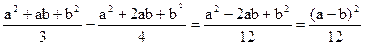
Рассмотренное в Примере 13 распределение является равномерным при a = 0
и b = 1.
2. Показательное (экспоненциальное) распределение:
Случайная величина x называется распределенной по показательному (экспоненциальному) закону с параметром 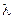 >0, если она непрерывного типа
>0, если она непрерывного типа
и ее плотность распределения задается формулой
f(x) = 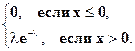 (10)
(10)
График функции приведен на Рис.11.
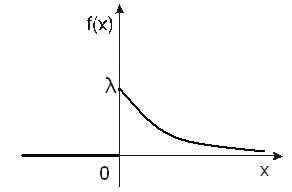
Рис. 11.
Математическое ожидание и дисперсия соответственно равны:
M (x) = 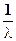 , D (x)=
, D (x)= 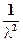
3. Закон нормального распределения.
Случайная величина называется распределенной по нормальному закону с параметрами а и 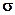 >0, если плотность распределения вероятностей имеет вид
>0, если плотность распределения вероятностей имеет вид
f(x) = 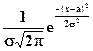 ,
, 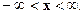
 (11)
(11)
Для того, чтобы построить график этой функции, проведем ее исследование. Вычислим производную
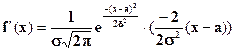 .
.
При x < a 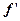 > 0, следовательно на интервале
> 0, следовательно на интервале 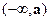 функция возрастает, а при x > a
функция возрастает, а при x > a 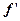 < 0, - функция убывает. В точке x = a – функция имеет максимум.
< 0, - функция убывает. В точке x = a – функция имеет максимум.
График функции приведен на Рис.12.
Важное значение в прикладных задачах имеет частный случай плотности нормального распределения при a = 0 и 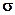 =1
=1
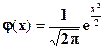 . (12) Функция (12) - четная, т.е.
. (12) Функция (12) - четная, т.е. 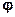 (-x) =
(-x) = 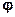 (x).
(x).
Для значений этой функции имеются таблицы (Приложение 1).
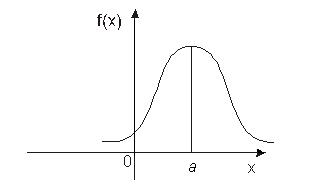
Рис. 12
Вычислим математическое ожидание и дисперсию:

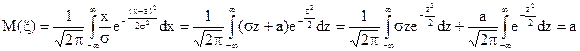
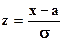 ;
; 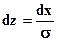 ;
; 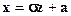 .
.
При вычислении интегралов использованы свойства:
1) 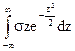 = 0, как интеграл от нечетной функции в симметричных пределах;
= 0, как интеграл от нечетной функции в симметричных пределах;
2) 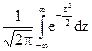 =1, как интеграл от плотности нормального распределения с параметрами a = 0 и
=1, как интеграл от плотности нормального распределения с параметрами a = 0 и 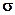 = 1 (свойство 2 функции плотности распределения).
= 1 (свойство 2 функции плотности распределения).
Аналогично можно показать, что D (x) = 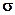 2. Параметры a и
2. Параметры a и 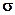 совпадают с основными характеристиками распределения. В дальнейшем, если плотность распределения случайной величины имеет вид (11),то для краткости будем записывать x ~ N (
совпадают с основными характеристиками распределения. В дальнейшем, если плотность распределения случайной величины имеет вид (11),то для краткости будем записывать x ~ N (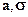 ).
).
Вероятность попадания случайной величины x в интервал 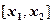 вычисляется по формуле (13)
вычисляется по формуле (13) 

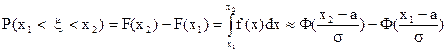 , (13)
, (13)
где 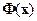 - функция Лапласа
- функция Лапласа
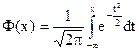 , ( 14)
, ( 14)
функция нормального распределения N(0,1),
д ля этой функции имеются таблицы (Приложение 2). Отметим, что
Ф(-x) = 1 - Ф(x) (15)
Пример 14. Коробки с шоколадом упаковывают автоматически.Их средняя масса равна 1,06 кг. Известно, что 5 % коробок имеют массу меньше 1 кг. Какой процент коробок, масса которых превышает 940 г. (вес коробок распределен нормально)?
Из условия задачи параметр а= 1,06, параметр 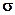 -неизвестен.
-неизвестен.
Рассмотрим случайную величину x - масса коробок. Требуется определить
p (x > 0,94), т.е. p (x > 0,94) = p (0,94 < x < + ∞) 
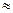
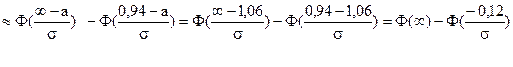
Из таблицы Приложения 2 определим 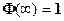 , по формуле (14) имеем
, по формуле (14) имеем
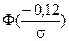 = 1-
= 1- 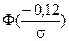 , тогда
, тогда
p (0,94 < x < + ∞) 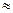 1-1+
1-1+ 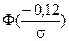 =
= 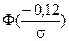 .
.
Параметр σ найдем из условия р (x < 1) = 0,5
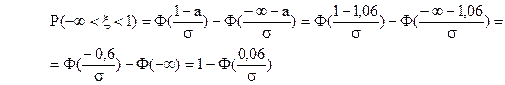
т.е. 1- 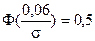 откуда получим
откуда получим 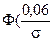 ) = 0,95.
) = 0,95.
По таблице Приложения 3 определим 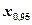 = 1,645, тогда из равенства
= 1,645, тогда из равенства
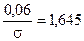 найдем значение
найдем значение 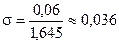 . Окончательно получим
. Окончательно получим
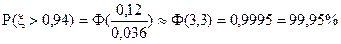 .
.
4. Распределение Парето
Распределение Парето используется при изучении распределения доходов, превышающих некоторый пороговый уровень x0.
f(x) = 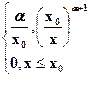 x0 < x < ∞, α > 0, х0 > 0 – параметры распределения.,
x0 < x < ∞, α > 0, х0 > 0 – параметры распределения.,
M(ξ)= 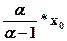 , D(ξ)=
, D(ξ)= 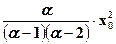 .
.
 2015-06-10
2015-06-10 3401
3401
