Пусть имеем несколько конечных множеств 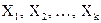 , причем
, причем 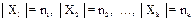 .
.
По теореме о мощности прямого произведения множеств, число векторов 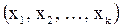 , которые можно составить из элементов данных множеств, равно
, которые можно составить из элементов данных множеств, равно 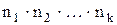 , так как
, так как
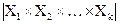 =
= 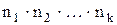 .
.
Полученный результат – один из важнейших в комбинаторике. Есть лишь одна тонкость. Иногда множество 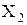 бывает не задано, а определяется после выбора
бывает не задано, а определяется после выбора 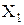 , а множество
, а множество 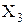 определяется после выбора элементов
определяется после выбора элементов 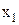 и
и 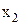 и т. д. Но при этом, как бы мы ни выбирали
и т. д. Но при этом, как бы мы ни выбирали 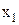 , выбор элемента
, выбор элемента 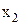 возможен
возможен 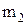 способами; при любом выборе
способами; при любом выборе 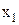 и
и 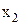 на третье место имеется некоторое число
на третье место имеется некоторое число 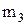 претендентов и т. д. И в этом случае ответ получится тот же самый:
претендентов и т. д. И в этом случае ответ получится тот же самый:
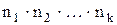 .
.
Пример. Сколько восьмизначных чисел можно построить из цифр (символов) (0, 1, 2... 9), так чтобы цифры не повторялись?
Так как речь идет именно о восьмизначном числе, а не о последовательности из 8 знаков, то, следовательно, 1-ая цифра не может быть нулем.
Тогда множество 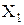 - кандидатов на 1-ое место содержит 9 элементов (1, 2,..., 9);после выбора первой цифры множество
- кандидатов на 1-ое место содержит 9 элементов (1, 2,..., 9);после выбора первой цифры множество 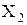 содержит снова 9 элементов - те цифры, которые не равны первой; если первая цифра
содержит снова 9 элементов - те цифры, которые не равны первой; если первая цифра
1, то (0, 2, 3... 9);
2, то (0, 1, 3... 9);
3, то (0, 1, 2, 4... 9)...
Множество 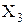 после выбора
после выбора 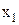 и
и 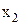 содержит 8 элементов - те цифры, которые не равны
содержит 8 элементов - те цифры, которые не равны 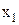 и
и 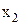 .Ответом является число
.Ответом является число 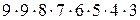 .
.
 2015-06-10
2015-06-10 634
634








