Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:
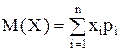 ,
,
где 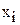 – значение дискретной случайной величины;
– значение дискретной случайной величины; 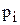 – вероятности принятия случайной величиной X значений
– вероятности принятия случайной величиной X значений 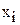 .
.
Если случайная величина принимает счетное множество возможных значений, то:
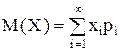 .
.
Математическое ожидание биномиально распределенной с параметрами n и p случайной величины:
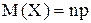 ,
,
где p - вероятность наступления события.
Свойства математического ожидания:
1. M(С) = C, где С – постоянная величина.
2. M(СX) = CM(X), где С – постоянный множитель.
3. M(X+Y) = M(X) + M(Y).
4. M(XY) = M(X) × M(Y), где X, Y – независимые случайные величины.
Дисперсией (рассеянием) случайной величины называется математи-ческое ожидание квадрата ее отклонения от ее математического ожидания:
Дисперсиядискретной случайной величины:
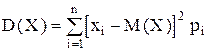
или 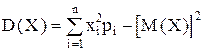 .
.
Дисперсия биномиально распределенной с параметрами n и p случайной величины:
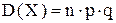 ,
,
где p - вероятность наступления события.
Свойства дисперсии:
1. D(C) = 0, где С – постоянная величина.
2. 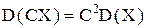 , где С – постоянный множитель.
, где С – постоянный множитель.
3. D(X+Y) = D(X) + D(Y), где X, Y – независимые случайные величины.
4. D(C+X) = D(X), где С – постоянная величина.
5. D(XY) = D(X)D(Y) + 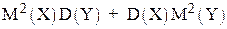 , где X, Y — независимые случайные величины.
, где X, Y — независимые случайные величины.
Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии:
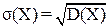 .
.
Свойства среднеквадратичного отклонения:
1. σ[C] = 0, где C = Const;
2. σ [C · X] = C · σ [X];
3. σ [X + Y ] =ABS(σ 2[X2] + σ 2[Y2 ])для независимых случайных величин X и Y.
Пример. В партии 10% нестандартных деталей. Наудачу отобраны 2 детали. Написать биномиальный закон распределения дискретной случайной величины Х - числа нестандартных деталей среди двух отобранных.
Решение. Дискретная случайная величина Х – число нестандартных деталей среди двух отобранных принимает следующие значения:
х1=0 – все детали стандартны из двух отобранных;
х2=1 – одна из двух отобранных деталей не стандартна;
х3=2 – обе отобранные детали нестандартны.
Так как вероятность отбора нестандартной детали p = 0,1 постоянная, то для определения вероятностей в соответствии с биномиальным законом распределения воспользуемся формулой Бернулли:
Pn(k)= 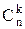 pk qn-k, где q = 1 – p = 0,9.
pk qn-k, где q = 1 – p = 0,9.
P2(0)= C 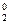 (0,1)0 (0,9)2=0,81,
(0,1)0 (0,9)2=0,81,
P2(1)=C 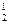 0,1 0,9=0,18,
0,1 0,9=0,18,
P2(2)=C 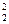 (0,1)2(0,9)0=0,01.
(0,1)2(0,9)0=0,01.
Проверяем условие нормировки 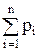 =1.
=1.
Имеем, что 0,81+0,18+0,01=1.
Искомый биномиальный закон распределения дискретной случайной величины Х имеет вид:
| х | ||||
| p | 0,81 | 0,18 | 0,01 |
По формуле:
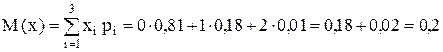 .
.
Тот же результат можно было получить, используя формулу
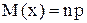 для нахождения математического ожидания биномиально распределенной дискретной случайной величины X.
для нахождения математического ожидания биномиально распределенной дискретной случайной величины X.
n = 2 – число испытаний;
p = 0,1 – вероятность успеха в каждом испытании;
M(X) = 2 × 0,1 = 0,2.
Дисперсию найдем по формуле:
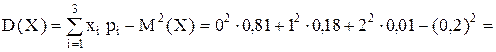
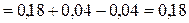 .
.
По формуле для дисперсии биномиального закона:
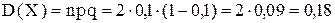 .
.
Пример. Дискретные случайные величины X и Y независимы и заданы распределениями:
| X | Y | ||||||
| p | 0,4 | 0,6 | p | 0,2 | 0,8 |
Найти распределение случайной величины Z = X + Y.
Решение. Найти закон распределения дискретной случайной величины, значит перечислить все ее возможные значения и рассчитать вероятности, с которыми она эти значения принимает. Значения случайной величины Z получаются путем сложения всех возможных попарных комбинаций значений случайных величин Х и Y.
0 + 1 = 1 0 + 2 = 2 1 + 1 = 2 1 + 2 = 3.
Таким образом, Z принимает три возможных значения: 1, 2 и 3. Найдем вероятности принятия величиной Z этих значений.
Так как Z принимает свое значение 1, тогда и только тогда, когда Х принимает значение 0, а Y – значение 1, то случайное событие «Z = 1» является произведением независимых (из-за независимости Х и Y по условию) случайных событий «Х = 0» и «Y = 1». Используя теорему умножения вероятностей независимых событий имеем:
P(Z=1)=P{(X=0)(Y=1)}=P(X=0)P(Y=1)=0,4  0,2=0,08=
0,2=0,08= 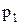 .
.
Так как Z принимает свое значение 2 либо когда X=0, а Y=2, либо когда X=1, а Y=1, причем одновременно это происходить не может, то событие «Z=2» – является суммой несовместных событий (X=0)(Y=2) и (X=1)(Y=1), и его вероятность можно найти с помощью теоремы сложения вероятностей несовместных событий:
P(Z=2)=P{(X=0)(Y=2)+(X=1)(Y=1)}=P{(X=0)(Y=2)}+P{(X=1)(Y=1)}=
=P(X=0)P(Y=2)+P(X=1)P(Y=1)=0,4  0,8+0,6
0,8+0,6  0,2=0,32+0,12=0,44=
0,2=0,32+0,12=0,44= 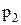 .
.
Рассуждая аналогично, найдем:
P(Z=3)=P{(X=1)(Y=2)}=P(X=1)P(Y=2)=0,6 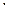 0,8=0,48=
0,8=0,48= 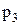 .
.
Проверим выполнение условия нормировки: 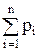 =0,08+0,44+0,48=1.
=0,08+0,44+0,48=1.
Таким образом, искомый ряд распределения имеет вид:
| Z | |||
| p | 0,08 | 0,44 | 0,48 |
 2015-06-10
2015-06-10 5245
5245








