2015-06-10
430
«Схема независимых испытаний Бернулли»
1. Схема Бернулли: основные составляющие условия.
2. Формула Бернулли.
3. Формула Пуассона. Условия применения.
4. Формула Муавра-Лапласа. Условия применения.
5. Интегральная теорема Лапласа. Условия применения.
6. Вероятность отклонения относительной частоты случайного события от его теоретической вероятности не более, чем на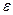 
.
7. Физический смысл формулы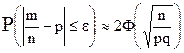 
.
8. Локальная функция Лапласа. Ее свойства. Ее график.
9. Интегральная не усеченная функция Лапласа. Ее свойства. Ее график.
10. Интегральная усеченная функция Лапласа. Ее свойства. Ее график.
Вопросы к самостоятельной работе № 1 по теме «Случайная величина»
1. Условие нормировки для непрерывной случайной величины.
2. Свойства плотности распределения вероятностей.
3. Связь между функцией распределения и плотностью распределения вероятностей непрерывной случайной величины.
4. Как ведут себя функция распределения и плотность распределения вероятностей в 
.
5. Записать плотность распределения вероятностей для равномерно распределенной в отрезке [3;8] случайной величины.
|
|
|
6. Записать функцию распределения для равномерно распределенной в отрезке [5;10] случайной величины.
7. Построить график плотности распределения вероятностей для равномерно распределенной в отрезке [0;4] случайной величины.
8. Построить график функции распределения для равномерно распределенной в отрезке [1;6] случайной величины.
9. Найти математическое ожидание и дисперсию для случайной величины, закон распределения которой задан плотность распределения вероятностей вида:
.
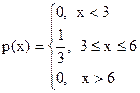10. Найти математическое ожидание и дисперсию для равномерно распределенной в отрезке [3;8] случайной величины.
11. Найти математическое ожидание и дисперсию для случайной величины, закон распределения которой задан плотность распределения вероятностей вида:
.
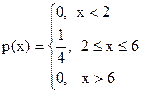12. Записать плотность распределения вероятностей для случайной величины, распределенной по показательному (экспоненциальному) закону с параметром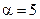 
.
13. Записать функцию распределения для случайной величины, распределенной по показательному (экспоненциальному) закону с параметром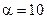 
.
14. Построить график плотности распределения вероятностей для случайной величины, распределенной по показательному (экспоненциальному) закону с параметром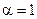 
.
15. Построить график функции распределения для случайной величины, распределенной по показательному (экспоненциальному) закону с параметром 
.
16. Найти математическое ожидание и дисперсию для случайной величины, закон распределения которой задан плотность распределения вероятностей вида:
|
|
|
.
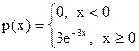17. Найти математическое ожидание и дисперсию для случайной величины, распределенной по показательному (экспоненциальному) закону с параметром .
18. Найти математическое ожидание и дисперсию для случайной величины, закон распределения которой задан плотность распределения вероятностей вида:
.
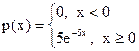19. Записать закон распределения для биномиальной случайной величины, распределенной с параметрами n=10, р=0,3.
20. Найти математическое ожидание и дисперсию биномиальной случайной величины, распределенной с параметрами n=5, р=0,5.
21. Дискретная случайная величина имеет закон распределения вида:
,
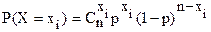где значения случайной величины хi = 0, 1, …, n, а n и р – параметры распределения. Записать формулу для нахождения ее математического ожидания и дисперсии.
22. Дискретная случайная величина имеет закон распределения вида:
,
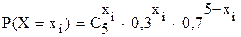где значения случайной величины хi = 0, 1, …, 5. Найти ее математическое ожидание и дисперсию.
23. Найти математическое ожидание и дисперсию случайной величины, распределенной по закону Пуассона с параметром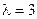 
.
24. Дискретная случайная величина имеет закон распределения вида:
,
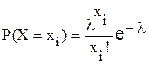где значения случайной величины хi = 0, 1, …, n …, а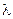 
– параметр распределения. Записать формулу для нахождения ее математического ожидания и дисперсии.
25. Дискретная случайная величина имеет закон распределения вида:
,
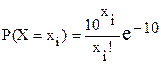где значения случайной величины хi = 0, 1, …, n, …. Найти ее математическое ожидание и дисперсию.
26. Случайная величина задана плотностью распределения вида:
.
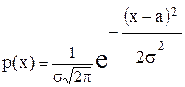Найти математическое ожидание и дисперсию.
27. Случайная величина задана плотностью распределения вида:
.
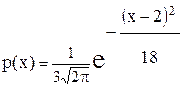Найти математическое ожидание и дисперсию.
28. Случайная величина задана плотностью распределения вида:
.
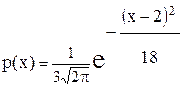В интервал с какими границами попадает эта величина с вероятностью 99,7%.
30. Дана случайная величина вида N [3; 2]. Найти математическое ожидание и дисперсию.
31.Дана случайная величина вида N [1; 5]. В интервал с какими границами попадает эта величина с вероятностью 99,7%.
