Вадной хар-кой СВ явл. хар-ка разброса значений СВ около мат.ожидания. Эта хар-ка называется дисперсией DX.
По определению дисперсия – это мат. ожидание квадрата отклонения СВ от ее MX: 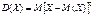
Если Х — ДСВ, то дисперсию вычисляют по следующим формулам:
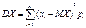
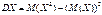
Св-ва дисперсии:
1. 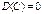
2. 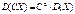
3. 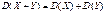
4. 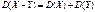
Среднее квадратическое отклонение дискретной случайной величины есть арифметическое значение корня квадратного из ее дисперсии:
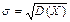 Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность
Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность
значений случайной величины
18. Биномиальный закон распределения и его числовые характеристики. Пусть проводится n независимых испытаний. В результате каждого из которых возможны 2 исхода: А – успех с вероятностью p, или 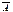 - неуспех с вероятностью q = 1-p. Дискретная СВ X,,характ. число появления события А принимает значения Х=m c вер-тями
- неуспех с вероятностью q = 1-p. Дискретная СВ X,,характ. число появления события А принимает значения Х=m c вер-тями
P(X=m)= 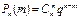 , где p>0, q>0, m
, где p>0, q>0, m 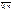 0,n. Для бин. з.р. доказано, что мат.ожидание M(X)= np, дисперсия
0,n. Для бин. з.р. доказано, что мат.ожидание M(X)= np, дисперсия 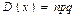 среднее квадратическое отклонение -
среднее квадратическое отклонение - 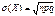
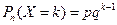 Т.о геометр.распр. есть испытание по схеме Бернулли до первого положительного исхода.Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем q=1-p (с этим связано название). Для геометр. закона распр. доказано, что мат. ожидание равно M(x)=1/p, дисперсия равна D(x)=
Т.о геометр.распр. есть испытание по схеме Бернулли до первого положительного исхода.Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем q=1-p (с этим связано название). Для геометр. закона распр. доказано, что мат. ожидание равно M(x)=1/p, дисперсия равна D(x)= 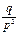 20. Гипергеометрическое распределение. Пусть имеется N элементов, из кот-х М эл-тов облад. некот-м признаком А. Извлек. случ. образом без возвращ-я n эл-тов. X – ДСВ, число эл-тов, облад. признаком А, среди отобр. n эл-тов. Вер-ть того, что Х =k опред. по формуле: P(x=k)=
20. Гипергеометрическое распределение. Пусть имеется N элементов, из кот-х М эл-тов облад. некот-м признаком А. Извлек. случ. образом без возвращ-я n эл-тов. X – ДСВ, число эл-тов, облад. признаком А, среди отобр. n эл-тов. Вер-ть того, что Х =k опред. по формуле: P(x=k)= 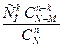 Для гипергеометр. распр. доказано, что M(x)=
Для гипергеометр. распр. доказано, что M(x)= 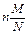 D(x)=
D(x)= 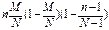

21. Формула Пуассона. Распределение Пуассона. Фактически, закон Пуассона – это биномиальное распр при большом числе испытаний n и малой вер-ти наступления события в каждом из испытаний, поэтому з-н Пуассона часто называют з-н редких явлений. ДСВ Х распр. по закону Пуассона, если она прин. знач. 0,1,2,..m,... с вер-тями 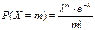 ,где λ=np (среднее число появл-я события в n испытаниях), m – число появления события в n независимых испытаниях; m приним. значения 0,1,2,…,n. Мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, совпадают и равны параметру λ: M(X)=λ, D(X)=λ.
,где λ=np (среднее число появл-я события в n испытаниях), m – число появления события в n независимых испытаниях; m приним. значения 0,1,2,…,n. Мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, совпадают и равны параметру λ: M(X)=λ, D(X)=λ.
22. Непрерывная случайная величина, плотность распределения вероятностей непрерывной случайной величины и ее свойства. Случ. вел-на Х наз. непрерывной, если ее функция распред-я непрерывна в любой точке и дифференцируема всюду, кроме отдельных точек. Пример: рост человека. Теорема: Вероятность любого отдельного знач-я непрер. случ. вел-ны равна нулю: P(X=x1)=0. Для НСВ P(x1< X < x2)=F(x2)-F(x1). НСВ как и ДСВ задается функцией распр. Однако,такой способ задания неперыв.СВ не единств. Для НСВ ввод. понятие плотности вер-ти. Р(Х) 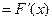 ). Свойства: 1.p(x)≥0 для люб, т.к. F(x) явл. неубывающей ф-ей.
). Свойства: 1.p(x)≥0 для люб, т.к. F(x) явл. неубывающей ф-ей.
2.Вер-ть попадания НСВ в инт-вал [а,b]вычисляется во формуле 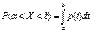
3. 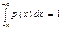 и
и 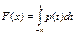
. График ф-ии p(x) называется кривой плотности вер-ти.
23. Математическое ожидание и дисперсия непрерывной случайной величины Мат.ожид. НСВ Х, знач., кот. х принадлежат (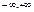 ) с плотностью вероят.р(х), вычисл. по формуле:
) с плотностью вероят.р(х), вычисл. по формуле: 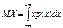 (требуется абсолют.сходимость интеграла.) Если НСВ X определена на[
(требуется абсолют.сходимость интеграла.) Если НСВ X определена на[ 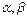 ],то мат.ожид. опред. по формуле
],то мат.ожид. опред. по формуле 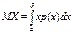
Дисперсия НСВ X, знач. кот. принадлежат инт-лу (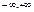 )с плотностью вер-ти р(Х) вычисляется по формуле:
)с плотностью вер-ти р(Х) вычисляется по формуле:
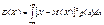 (требуется абс. сход. интеграла)
(требуется абс. сход. интеграла)
Если все знач. НСВ принадлежат инт-лу (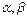 ), то дисперсия вычисл.по формуле:
), то дисперсия вычисл.по формуле: 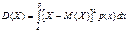
Или равносильным рав-вом:
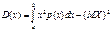
24. Равномерный закон распределения и его числовые характеристики Непр. случ. велич.х распред. равномерно на отрезке [а;b], если её плотность вероятности р(х) постоянна на этом отрезке и равна 0 вне его:
Р(х)= {1/ (b-a), при а< =х<=b,
{О, при х<а, х>b
Пример: ожидание транспорта на остановке.
Функция распред. случайн. величины, распред-ой по равномерн. закону, имеет вид:
F(x)= { O, x<=a,
{(x-a)/(b-a), a<=x<=b,
{1, x>b
Мат. ожидание, дисперсия, средн. кв. откл-е:МХ=(а+b)/2; DХ= 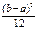 ,
, 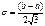
25. Показательный закон распределения и его числовые характеристики. Непрерывная СВ Х имеет показ. (экспоненциальное) распределение с параметром λ >0, если ее плотность распред-я имеет вид: 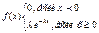
Ф-ция распределения СВ, распределенной по показ. з-ну: 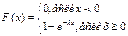
Показательному распределению обычно подчиняется время ожидания в очереди. Вероятность попадания случайной величины Х на интервал (α;β)
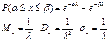
26. Нормальный закон распределения. Влияние параметров распределения на вид нормальной кривой. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и 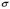 , если её плотность вероятности имеет вид p(x)=
, если её плотность вероятности имеет вид p(x)= 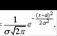 Кривая нормального распределения p(x) (нормальная кривая или кривая Гаусса) приведена на рисунке.
Кривая нормального распределения p(x) (нормальная кривая или кривая Гаусса) приведена на рисунке.
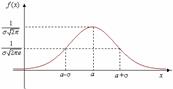
В точке х=a функция достигает своего максимума, кот. равен 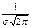 График симметр. относит. а. При изменении параметра а форма кривой не меняется, а ее график сдвигается влево или вправо. При изменении параметра σ меняется форма нормальной кривой: с увеличением параметра σ кривая должна приближаться к 0Х и растягиваться вдоль этой оси, а с уменьшением σ кривая стягивается к прямой х=а.
График симметр. относит. а. При изменении параметра а форма кривой не меняется, а ее график сдвигается влево или вправо. При изменении параметра σ меняется форма нормальной кривой: с увеличением параметра σ кривая должна приближаться к 0Х и растягиваться вдоль этой оси, а с уменьшением σ кривая стягивается к прямой х=а.
27. Числовые характеристики случайной величины, имеющей нормальное распределение. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и  , если её плотность вероятности p(x) имеет вид p(x)=
, если её плотность вероятности p(x) имеет вид p(x)= 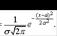 : Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а её дисперсия - квадрату параметра
: Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а её дисперсия - квадрату параметра  , т.е.
, т.е. 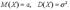 Величина М(Х) называется также центром рассеяния, а среднеквадратичное отклонение
Величина М(Х) называется также центром рассеяния, а среднеквадратичное отклонение  характеризует ширину кривой распределения. С возрастанием
характеризует ширину кривой распределения. С возрастанием  максимальная ордината кривой убывает, а сама кривая становится более пологой, растягиваясь вдоль оси абсцисс, тогда как при уменьшении
максимальная ордината кривой убывает, а сама кривая становится более пологой, растягиваясь вдоль оси абсцисс, тогда как при уменьшении  кривая вытягивается вверх, одновременно сжимаясь с боков
кривая вытягивается вверх, одновременно сжимаясь с боков
 2015-06-10
2015-06-10 3753
3753
