Вер-ть попад-я в зад. интервал нормально распред. случ. в-ны. В-сть зад. откл-я. Правило трех сигм

Ф-ия распр. нормального распр. СВ Х выражается через ф-ию Лапласа по формуле:

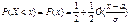
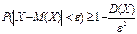В-сть попадания нормально распр. СВ Х в заданный интервал 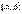опр.ф-лой. 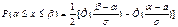Часто в задачах требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х от ее М(х) =а по абсол. величине меньше заданного полож. числа ε. Для этого исп. формула:

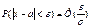
При реш-и многих важных практич. задач делают предпол-е, что СВ распределена по норм. закону. Возн. вопрос, на каком основании делается такое допущение. Для иссл-я этого вопроса рассм. одну характ. особ-сть норм. распред-я СВ. Найдем в-сти событий: |x-a|<σ;|x-a|<2σ; |x-a|<3σ Используем формулу:P(|x-a|<σ)=2Ф(1)=0,6826 P(|x-a|<2σ)=2Ф(2)= 0,9594 P(|x-a|<3σ)=2Ф(3)=0,9973 – это событие практически достоверное. Посмотрим в таблицу: из последнего соотношения следует, что практически все возможные значения норм. распр-я СВ x принадлежат интервалу (a-3σ; a+3σ)

Итак, правило трех σ утверждает, что с очень высокой вер-тью (0,998) практически все значения СВ сосредоточены в инт-ле (a-3σ;а+3σ)