Предельные теоремы в схеме Бернулли

1. Предельная теорема Пуассона. При р»0, n-велико, np= l £ 10.

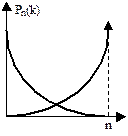
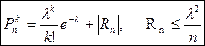
Формула дает распределение Пуасона, описывает редкие события.

2. Предельная теорема Муавра-Лапласа.

0 £ p £ 1, n –велико, np>10

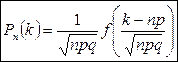
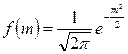- стандартное нормальное распределение

3. Предельная интегральная теорема Муавра-Лапласа.

В условиях предыдущей теоремы вероятность того, что событие А в серии из n испытаний наступит не менее k₁ раз и не более k₂ раз:

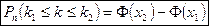
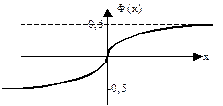
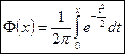- функция Лапласа

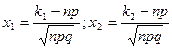
Следствие:

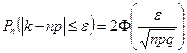
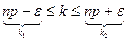
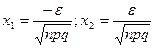
Случайная – величина, которая в ходе опыта принимает то или иное значение из возможных своих значений, меняющееся от опыта к опыту и зависящее от множества непредсказуемых факторов.

Если случайные события характеризуют процесс качественно, то случайная величина – количественно.

Случайная величина – численная функция, задаваемая на множестве элементарных событий. На одном множестве может быть несколько случайных величин.

Дискретная случайная величина (ДСК) – величина, принимающая счетное (конечное или бесконечное) множество значений.

Непрерывная случайная величина (НСВ) – случайная величина, значения которой образуют несчетные множества. (Например, расход бензина на 100 км у автомобиля Жигули в Нижнем Новгороде).

Задать св – значит указать все множество ее значений и соответствующие этим значениям вероятности. Говорят, что задан закон распределения случайной величины.

Случайная величина может быть задана несколькими способами:

1. Табличный.

Х	a1	a2	…	аn
Р	p1	p2	…	pn

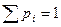
Значения случайных величин в таблице ранжируются, т.е. указываются в порядке возрастания.

Недостпаток табличного способа в том, что он пригоден только для случайных величин, принимающих небольшое количество значений.

2. Функция распределения F(x) = P(X<x) или интегральный закон распределения.

Указывается вероятность того, что случайная величина принимает значение < x.

Х	a1	a2	a3	…	аn-1
Р	p1	p2	p3	…	pn-1
F(x)	p1	p1+p2	p1+p2+p3	…	p1+p2+…+pn-1

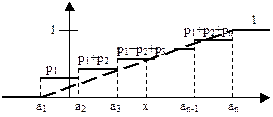
При увеличении значения случайной величины, количество ступенек функции F(х) возрастает, уменьшается их высота и в пределе при 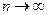получаем гладкую непрерывную функцию F(х).

Свойства функции F(х).

1. Неотрицательна. 0£ F(х)£1

2. Неубывающая F(х₂)> F(х₁) при х₂>х₁

3.

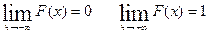
4. Р(a<x<b) = F(a) – F(b) Вероятность того, что значение х попадет в интервал (а,b) определяется разностью значений функции на концах интервала.

Наряду с F(х) вводится f(x) - функция плотности вероятности или дифференциальный закон распределения:

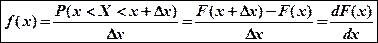
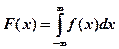
Свойства функции f(x):

1. Неотрицательна. (т.к. F(x) неубывающая, f(x)³0)

2. Площадь фигуры под кривой на интервале (a,b) равна: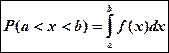

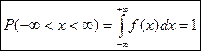- условие нормировки функции f(x).