§ Элементарные события (элементы 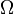 ), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.
), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.
§ Каждое случайное событие (элемент 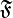 ) — это подмножество
) — это подмножество 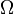 . Говорят, что в результате эксперимента произошло случайное событие
. Говорят, что в результате эксперимента произошло случайное событие 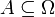 , если (элементарный) исход эксперимента является элементом
, если (элементарный) исход эксперимента является элементом 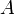 .
.
Требование, что 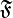 является сигма-алгеброй подмножеств
является сигма-алгеброй подмножеств 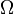 , позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.
, позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.
Простым и часто используемым примером вероятностного пространства является конечное пространство. Пусть 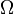 — конечное множество, содержащее
— конечное множество, содержащее 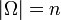 элементов.
элементов.
В качестве сигма-алгебры удобно взять семейство подмножеств 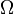 . Его часто символически обозначают
. Его часто символически обозначают 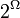 . Легко показать, что общее число членов этого семейства, т.е. число различных случайных событий, как раз равно
. Легко показать, что общее число членов этого семейства, т.е. число различных случайных событий, как раз равно 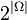 , что объясняет обозначение.
, что объясняет обозначение.
Вероятность, вообще говоря, можно определять произвольно. Часто, однако, нет причин считать, что один элементарный исход чем-либо предпочтительнее другого. Тогда естественным способом ввести вероятность является:
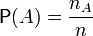 ,
,
где 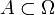 , и
, и 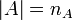 - число элементарных исходов, принадлежащих
- число элементарных исходов, принадлежащих 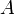 .
.
В частности, вероятность любого элементарного события:
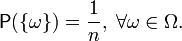
 2015-06-10
2015-06-10 431
431







