2015-06-10
713
Выделим из тензора скорости деформации новый тензор, который связан только с изменением формы и называется девиатором скорости деформации
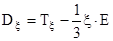(2.10)
где Е – единичный тензор.
Компоненты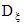 
определяются соотношениями
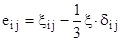(2.11)
или более подробно
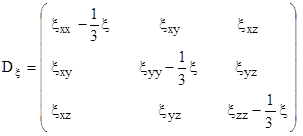(2.12)
Тензор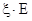 
- называется шаровым и соответствует только изменению объема.
Главные направления девиатора скорости деформации 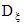и тензора скорости деформации 
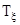совпадают. Это следует из соотношения (2.10), так как для единичного тензора Е главным направлением будет любое направление.
Если материал несжимаем (довольно распространенная гипотеза), то
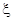=0 и =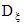
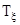
то есть в этом случае компоненты девиатора и тензора скорости деформации совпадают
,
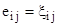а соотношение
= 
+ 
+ 
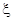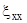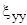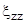= 0 или = 
+ 
+ 
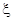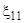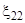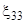=0 (2.13)
представляет собой условие несжимаемости.
Инварианты девиатора скорости деформации имеют вид
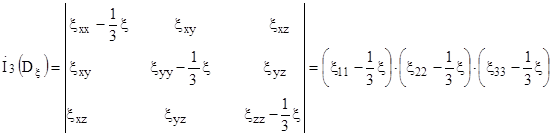
Большую роль в теории пластичности играет второй инвариант, неотрицательную величину, составленную из которого
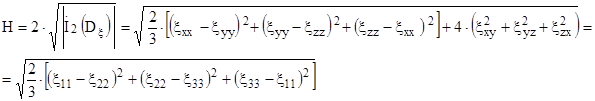.(2.15)
называют интенсивностью скоростей деформации сдвига. В тензорной форме для несжимаемого материала она запишется так
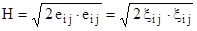(2.16)
Интенсивность скоростей деформации сдвига обращается в нуль, если материал равномерно расширяется или сжимается, когда
= = .
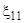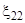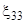Для чистого сдвига, когда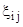 
=0, кроме, например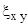 
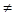0
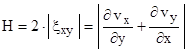
Для одноосного растяжения или сжатия несжимаемого материала, когда 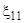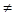0,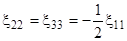 
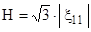
Уравнение неразрывности определяет монотонность процесса деформации и отсутствие нарушения сплошности (разрывов и т.п.) в деформируемом теле.
Данное уравнение выводится как следствие закона сохранения массы тела в процессе деформации
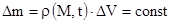(2.17)
Здесь 
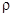- массовая плотность; 
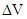- объем малой окрестности, окружающей точку М; 
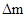- её масса. Скорость частицы в точке М - 
.
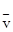Исходя из отмеченных условий процесса деформации функци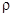и и 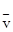предполагаются непрерывными и достаточное число раз дифференцируемыми функциями своих аргументов.
Уравнение неразрывности имеет вид
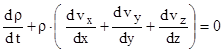(2.18)
В частном случае несжимаемого материала (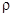 =const) оно переходит в следующее уравнение
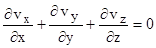(2.19)
или, что то же самое
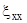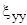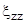+ + =0
и представляет собой условие несжимаемости (отмеченное ранее).
Уравнение непрерывности и рассмотренные ранее дифференциальное уравнения движения еще не образуют замкнутой системы уравнений, так как четыре уравнения содержат десять неизвестных (шесть компонентов тензора напряжений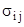 
, плотность 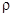и три компоненты вектора скорости vi).
Несколько позднее эта система будет замкнута путем введения шести физических уравнений, которые не содержат дополнительных неизвестных, а объединяют напряжения и скорости движения.
