Разбиение множества на классы. Классификация

В процессе изучения предметов и явлений окружающего мира мы постоянно сталкиваемся с классификацией. Классификация широко используется в биологии, химии, математике, языке и многих других науках. Она облегчает процесс усвоения знаний.

Классификация в любой области человеческой деятельности связана с разбиением множества на подмножества (классы). Например, классификация частей речи, членов предложения, чисел, геометрических фигур и так далее.

Полученные подмножества должны обладать некоторыми свойствами:

1) они не должны быть пустыми;

2) не должны содержать общих элементов;

3) объединение всех подмножеств должно равняться самому множеству.

Определение: Классификацией или разбиением множества на классы называется представление этого множества в виде объединения непустых попарно непересекающихся своих подмножеств.

Для примера рассмотрим классификацию с помощью двух свойств.

Пусть U –множество студентов лингвистического института РГПУ, свойство α - «быть отличником», свойство β - «быть спортсменом». С помощью указанных свойств можно выделить следующие подмножества:

А – множество отличников;

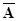– множество не отличников;

В – множество спортсменов;

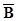– множество не спортсменов.

IV

Множество U в этом случае оказывается разбитым на следующие четыре класса (подмножества):

II

I – множество отличников-спортсменов;

I I – множество отличников - не спортсменов;

II

III

I

I – множество не отличников - спортсменов;

IV – множество не отличников - не спортсменов;

Рис. 2

U A B

Можно доказать, что если n – число свойств, то максимальное число классов в разбиении равно 2ⁿ.

Число элементов объединения и разности двух конечных множеств

Пусть A и B – конечные множества. Число элементов множества A условимся обозначать символом m ( A ) и называть численностью множества A.

Определим численность объединения множеств A и B.

Если множества A и B не пересекаются (см. рис. 1а), то m(A È B) = m(A) + m(B). Таким образом, численность объединения конечных непересекающихся множеств равна сумме численностей этих множеств.

Если множества A и B пересекаются (см. рис. 1б), то в сумме m(A) + m(B) число элементов пересечения A Ç B содержится дважды: один раз в m ( A ), а другой – в m ( B ). Поэтому, чтобы найти численность объединения m(A È B), нужно из указанной суммы вычесть m(A Ç B). Таким образом:

m(A È B) = m(A) + m(B) - m(A Ç B)

Определим теперь численность разности множеств A и B.

Если множества A и B не пересекаются (см. рис. 1а), то A \ B = A, и поэтому m(A \ B) = m(A).

Если множества A и B пересекаются (см. рис. 1б), то m(A \ B) = m(A) - m(A Ç B).

Если В Ì А (см. рис. 1в), то A Ç B = B, и, следовательно, m(A \ B) = m(A) - m(B).