Из 20 вопросов программы студент выучил 16. Требуется найти вероятность того, что 3 предложенных вопроса окажутся знакомыми (событие 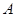 ).
).
Решение
Обозначим 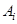 - событие «
- событие «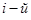 вопрос оказался знакомым» (
вопрос оказался знакомым» (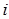 = 1, 2, 3). Тогда
= 1, 2, 3). Тогда 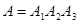 . Можно представить, что вопросы записаны на отдельных карточках и выбираются наугад один за другим (без возвращения). Тогда
. Можно представить, что вопросы записаны на отдельных карточках и выбираются наугад один за другим (без возвращения). Тогда 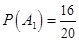 ,
, 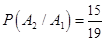 (вероятность получения второго знакомого вопроса при условии, что первый оказался знакомым),
(вероятность получения второго знакомого вопроса при условии, что первый оказался знакомым), 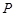 (вероятность третьего «везения» при условии, что знакомыми оказались оба первых вопроса). По формуле (3.9)
(вероятность третьего «везения» при условии, что знакомыми оказались оба первых вопроса). По формуле (3.9)
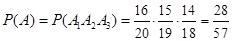 .
.
События 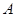 и
и 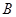 называются независимыми (нужно не путать с несовместными), если выполняется условие
называются независимыми (нужно не путать с несовместными), если выполняется условие
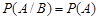 , ,
| (3.11) |
или эквивалентное ему условие
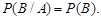
| (3.12) |
На практике независимость событий означает, что появление одного из них не изменяет вероятности другого или появление одного из них не несет информации, о другом.
События 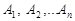 называются независимыми, если каждое из них не зависит от каждого из остальных и от всевозможных произведений остальных событий.
называются независимыми, если каждое из них не зависит от каждого из остальных и от всевозможных произведений остальных событий.
Для независимых событий теорема умножения принимает простой вид
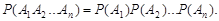
| (3.13) |
В частности, для двух независимых событий
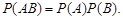
| (3.14) |
 2015-06-10
2015-06-10 315
315








