2015-06-10
1671
1. Постановка задачи и математическая модель
Оболочка – деталь, у которой один размер (толщина t) меньше двух других. Примеры – тонкостенная труба, сосуд иди резервуар, ведро, корпус ракеты.
Примером точного решения является задача Ламе для трубы. Пренебрегая толщиной, получаем приближенное решение для напряжений в срединной поверхности радиусом R
.
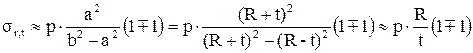Т.е. напряжениями по нормали к поверхности можно пренебречь в сравнении с нормальными напряжениями в срединной поверхности. Напряжения в сечении ввиду малости t постоянны, т.е в сечениях не возникают изгибающие моменты (безмоментная теория). Расчет при таких допущениях, обобщенный для осесиметричных оболочек, предложен Лапласом. Рассмотри его подробно.
Осесиметричная оболочка – симметрична относительно оси как геометрически, так и по характеру приложения внешней нагрузки – давления. Например, боковая поверхности ведра, стоящего на плоскости - осесиметрична, а когда его поднимают за дужку – не осесиметрична.
Срединная поверхность имеет два радиуса кривизны: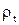 
в цилиндрическом сечении и 
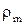в меридиональном(осевом) сечении. Например, у трубы 
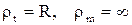. Схема напряжений для бесконечно малого элементы, выделенного двумя осевыми и двумя цилиндрическими сечениями, представлена на рисунке.
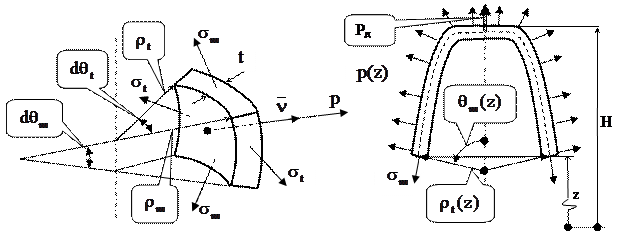Составим уравнение равновесия сил вдоль нормали 
:
.
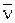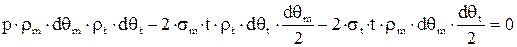После преобразования получаем уравнение Лапласа
.
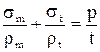Второе уравнение можно получить, проектируя силы в цилиндрическом сечении на ось оболочки с учетом силы Рд на днище
.
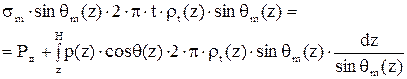После преобразования
.
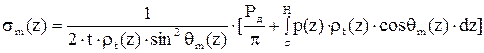2. Примеры
· Шаровая оболочка радиусом R при постоянном давлении
· 
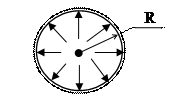
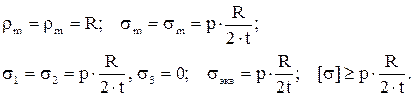
Цилиндрическая оболочка радиусом R с днищами при постоянном давлении
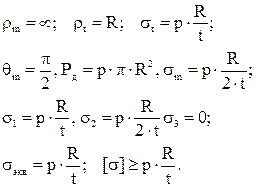
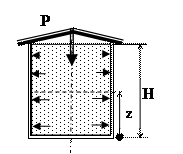
· Оболочка - резервуар радиусом R и высотой Н, заполненный жидкостью удельным весом γ
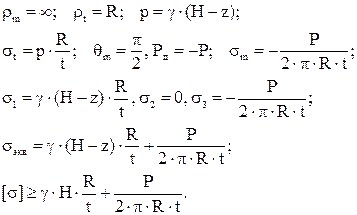
· Полусферическая оболочка-резервуар, заполненная жидкостью удельным весом γ
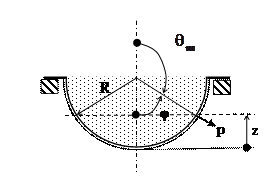
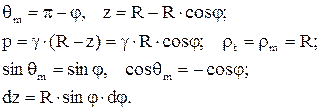
Подставляем в выражение для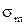 
. Для упрощения вычислений находим напряжения в нижней части, где Рд =0, т.е изменяем направление интегрирования
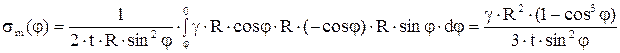Из уравнения Лапласа
.
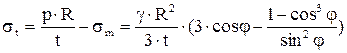
Значения 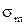всегда положительны. Значения 
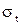при φ=0 положительны и раны 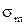, а при φ=π/2 – отрицательны (верхнее «кольцо» сжимается под тяжестью жидкости). При этом эквивалентные напряжения максимальны и равны 
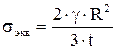. В нижней точке 
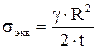, т.е. такое же как в сфере под давлением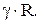 
· Цилиндрическая оболочка-резервуар, заполненная жидкостью удельным весом γ
.
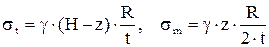
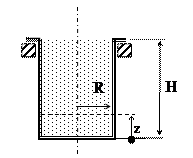Оба напряжения положительны. Максимумы наблюдаются в противоположных точках по z. Поэтому опасные эквивалентные напряжения равны максимуму из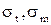 
и зависят от величины Н. При равных объемах сферического и цилиндрического резервуаров 
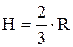. Максимальные эквивалентные напряжения равны.
При относительно большой толщине оболочки изгибающими моментами в сечении нельзя пренебречь. Моментную теорию осесиметричных оболочек рассмотрим на примере расчета круглых осесиметричных пластин частного случая оболочек.
