Циркуляция вектора магнитной индукции

Циркуляцией вектора 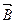по заданному замкнутому контуру называется интеграл

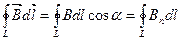
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора 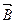): Циркуляция вектора 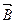по произвольному замкнутому контуру равна произведению магнитной постоянной 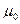на алгебраическую сумму токов, охватываемых этим контуром:

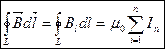, где

n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.

Например:

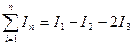
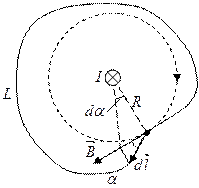Продемонстрируем справедливость теоремы о циркуляции вектора 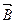на примере магнитного поля прямого тока I, перпендикулярного плоскости чертежа и направленного от нас:

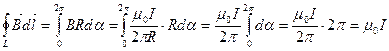
Таким образом, исходя из теоремы о циркуляции вектора 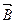получили выражение для магнитной индукции поля прямого тока, выведенное выше.