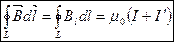Закон полного тока для магнитного поля в веществе

, где

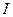и 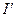– соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым контуром L.

Циркуляция вектора магнитной индукции 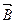по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор 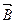характеризует результирующее поле, созданное как макроскопическими токами в проводниках (токами проводимости), так и микроскопическими токами в магнитиках, поэтому линии вектора магнитной индукции 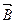не имеют источников и являются замкнутыми.

Докажем, что циркуляция намагниченности 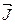по произвольному замкнутому контуру L равна алгебраической сумме молекулярных токов, охватываемых этим контуром:

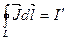
Тогда закон полного тока для магнитного поля в веществе запишем в виде:

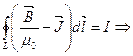
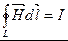– теорема о циркуляции вектора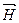

Циркуляция вектора 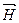по произвольному замкнутому контуру L равна алгебраической сумме токов проводимости, охватываемых этим контуром.