2015-06-10
511
1.1. 10; 1.2. 63; 1.3. 3024; 1.4. 99999; 1.5. 36; 1.6. а) 120, б) 120; 1.7. 1680; 1.8. 5040; 1.9. 2058; 1.10. а) 24310, б) 45; 1.11. 1024000; 1.12. 2520; 1.13. 720; 1.14. 382; 1.15. 125; 1.16. 729; 1.17. 756; 1.18. 300; 1.19. 215760; 1.20. 750.
Классическое и статистическое определение вероятности
2.1. 180; 2.2. P(A) =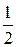 
, Р(В) = 
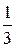; 2.3. 
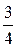; 2.4. Р(А) = 
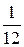, Р(В) = 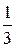; 2.5. 
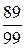; 2.6. 
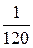; 2.7. 
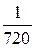; 2.8. 
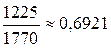; 2.9. 
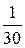; 2.10. 
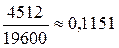; 2.11. 
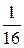; 2.12. а) 
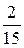, б)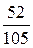 
; 2.13. 
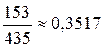; 2.14. 
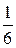; 2.15. Р(А) = 
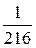, Р(В) = 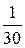, Р(С) = 
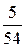; 2.16. а) 
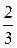, б)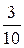 
; 2.17. Р(А) = 
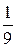, Р(В) = 
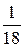; 2.18. 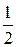; 2.19. 
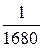; 2.20. 
.
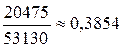Операции над событиями
3.1. А – в группе нет ни одного бракованного изделия, В – в группе либо нет бракованных изделий, либо одно бракованное изделие; 3.2. А+В = А, АВ = В; 3.3. Ω = {ГГГ; ГГЦ; ГЦГ; ЦГГ; ГЦЦ; ЦГЦ; ЦЦГ; ЦЦЦ}; А = {ГГГ; ГГЦ; ГЦГ; ЦГГ }; 
3.4. В = А6 , С = А5 ; 3.5. а) АВС, б) АВС, в) АВС, г) А+В+С, д) АВ+АС+ВС, е) АВС+АВС+АВС, ж) АВС+АВС+АВС, з) АВС, и) АВС; 3.7. А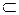 
ВС, б) В 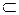А и С 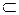А; 3.8. С = АВ, Д = АВ+АВ, Е = А+В; 3.9. В = А1+А2+А3, С = А1А2А3 , D = А1А2А3 + А1А2А3 + А1А2А3, Е = А1А2А3 + А1А2А3 + А1А2А3, F = А1А2А3 + А1А2А3 + А1А2А3 = А1А2 + А1А3 + А2А3 ; 3.10. а) да, б) нет, в) да.
Теоремы сложения и умножения вероятностей
4.1. 0,28; 4.2. 0,2; 4.3. (0,85)3= 0,614125; 4.4. 0,92; 4.5. а) 0,512, б) 0,992, в) 0,384; 4.6. Р(А) = 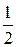; Р(В) = 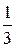, события А и В независимы; 4.7. 
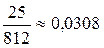; 4.8. 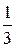; 4.9. 0,7; 4.10. Р(А) = 
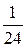, Р(В) = 1, Р(С) = 
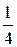, Р(D) = 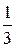, Р(Е) = 
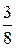; 4.11. 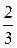; 4.12. 0,55; 4.13. 
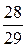; 4.14. 0,8; 4.15. Первая технология (Р = 0,49896, Р = 0,392).
Формулы полной вероятности и Бейеса
5.1. 0,7; 5.2.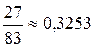 
; 5.3. 0,52; 5.4. 0,25; 5.5. 0,0022; 0,11; 5.6. 
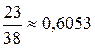; 5.7. 0,6044; 5.8. 0,675; 5.9. 
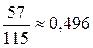; 5.10. 0,9999; 5.11. 0,022; 5.12. 
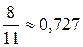; 5.13. а) 0,4, б) 0,3; 5.14. 0,3888; 5.15. 0,5.
