 Привести пример таких множеств А, В, С, что А Ì В, В Ì С, но А Ì С.
Привести пример таких множеств А, В, С, что А Ì В, В Ì С, но А Ì С.
Основные операции над множествами. Диаграммы Эйлера-Венна
Задание N 20
Даны множества 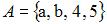 и
и 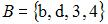 . Тогда истинными высказываниями являются…
. Тогда истинными высказываниями являются…
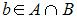 | |
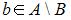 | |
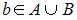 | |
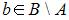 |
Задание N 21
Множества А, В и С изображены на диаграмме.
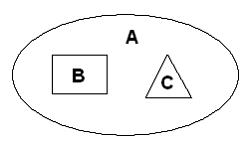
Тогда для них верны следующие высказывания
A 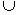 B=B B=B | |
B 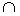 C=B C=B | |
A 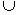 B=A B=A | |
B 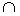 C= C=  |
Задание N 22
Даны два множества: 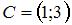 – интервал числовой оси;
– интервал числовой оси; 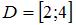 – отрезок числовой оси. Тогда для них истинными высказываниями являются…
– отрезок числовой оси. Тогда для них истинными высказываниями являются…
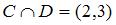 | |
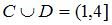 | |
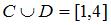 | |
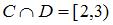 |
Задание N 23
Заданы произвольные множества А, В и С. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.
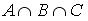
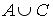
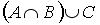
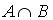
 2015-06-10
2015-06-10 782
782








