Пример использования графического метода решения

Задачи линейного программирования могут решаться графически, если переменных только 2-е, аналитически (в ручную), при матрицах небольших размеров, автоматически с использованием специальных пакетов программ.

Графический метод линейного программирования является наиболее простыми очень наглядным методом решения задач линейного программирования.

Рассмотрим применение этого метода на примере расчета оптимальной загрузки судна двумя видами груза.

Введем следующие обозначения:

q₁,q₂ - количество принимаемых к перевозке грузов, в тоннах.

u₁,u₂ - удельная грузовместимость, в м³/тонну.

Dч- чистая грузоподъемность судна, в тоннах.

W- объем грузового помещения судна (грузовместимость), в м³.

C₁,C₂ - стоимость фрахта за перевозку одного груза, в [у. е.].

Математическая модель задачи:

L=S Ci*Xi ® max (2.3.1.)

Ограничения:

по грузовместимости судна: q₁ + q₂ £ Dч (2.3.2.)

по грузоподъемности судна: q₁ u₁ + q₂ u₂ £ W (2.3.3.)

по массе отдельных грузов: Q_1min £ q₁ £ Q_1max (2.3.4.)

Q_2min £ q₂ £ Q_2max

по объему отдельного вида груза:

W_1min £ u₁ q₁ £ W_1max (2.3.5.)

W_2min £ u₂ q₂ £ W_2max

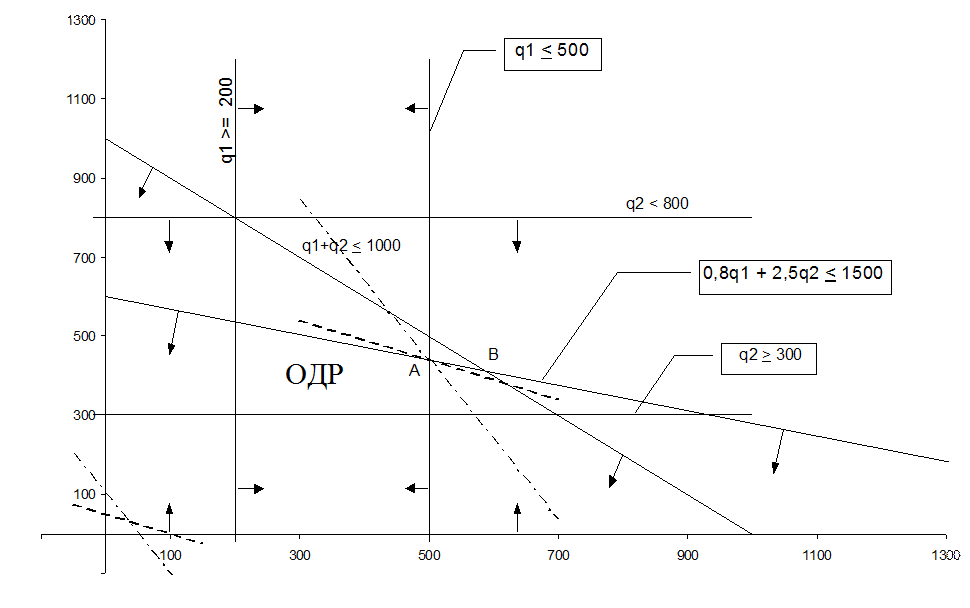
Задача решается следующим образом. В декартовой системе координат q₁, q₂, выбирается масштаб построения. На положительной части q₁, q₂, обозначаются линии, соответствующие границам неравенств, для чего неравенство превращаем в равенство (т. е. q₁ + q₂ £ Dч ® q₁ + q₂ = Dч, и так со всеми остальными неравенствами). На линиях границ обозначим область, удовлетворяющую соответствующим неравенствам. Определим область допустимых решений. Любая точка в ОДР имеет координаты удовлетворяющие условиям задачи.

Для определения оптимальных значений q₁ и q₂ строят направление целевой функции L, и приравнивают её к любому положительному числу. Построя направление L, перемещаем её параллельно самой себе до соприкосновения с самой отдаленной от начала построения точкой ОДР. Координаты этой точки дают оптимальное решение q_o1, q_o2. После определения q_o1, q_o2 анализируется полученный результат.

Рассмотрим конкретный пример оптимальной загрузки судна двумя видами груза.

Dч =1000тонн

W =1500м³

u₁ = 0,8 м³/тонн u₂ = 2,5 м³/тонн

Q_1min=200 тонн Q_2min= 300 тонн

Q_!max=500 тонн Q_2max= 800 тонн

W_1min=---- м³ W_2max=----- м³

W_1min=---- м³ W_2max-=---- м³

C₁= 10 у.е./т C₂= 20 у.е./т

где / ---- / - означает "нет ограничения".

q_o1+ q_o2 < 1000 (2.3.6.)

0,8q_o1+2,5q_o2 < 1500 (2.3.7.)

200£ q_o1 £ 500 (23.8.)

300 £ q_o2 £ 800 (2.3.9.)

Математическая модель полной загрузки судна представлена уравнениями (2.3.6.) и (2.3.7.). Решая эти уравнения совместно, найдем количество груза обоих видов, обеспечивающих полную загрузку:

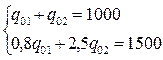
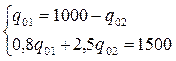
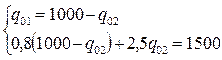
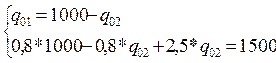
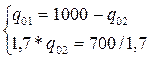
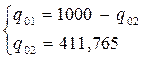
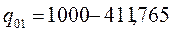
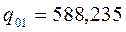
Таким образом, для полного использования и грузовместимости судна, на борт необходимо погрузить 588,235 тонн первого груза q_o1 и 411,765 тонн второго груза q_o2. То есть:

q_o1 = 588,235 т

q_o2 = 411,765 т

При этом значение целевой функции будет следующим:

L₁ = S Ci*Xi = C₁ * q₁+ C₂ * q₂ = 10*588,235+20*411,765 = 14117,65 у.е.

Далее производим следующее: наносим оси q₁ и q₂ в декартовой системе координат; выбираем масштаб построения одинаковый для обеих осей; превращаем неравенства 2.3.6.-2.3.9. в равенства, которые представляют собой уравнения прямых:

q_o1+ q_o2 =1000 (2.3.10.)

0,8q_o1+2,5q_o2 =1500 (2.3.11.)

200 = q_o1 = 500 (2.3.12.)

300 = q_o2 = 800 (2.3.13.)

Затем строим эти прямые в декартовой системе и находим область, удовлетворяющую соответствующим неравенствам 2.2.6.-2.2.9. Эта область и является Областью Допустимых Решений (ОДР), любая точка которой удовлетворяет условиям задачи.

Целевую функцию L = S Ci*Xi = C₁ * q₁+ C₂ * q₂ приравниваем к любому положительному числу – в нашем случае:

Lопт_х = 10 * q₁+ 20 * q₂ = 1000,

и строим эту прямую. Потом перемещаем ее параллельно самой себе до прикосновения с самой отдаленной от начало построения точкой – в нашем случае это точка "А". Координаты этой точки "А" дают оптимальное решение q_o1, q_o2. Сняв значения q_o1, q_o2, анализируем полученный результат. Для этого находим значение целевой функции при полученных q_o1, q_o2:

q_o1 = 500 т

q_o2 = 440 т

L опт = S Ci*Xi = C₁ * q₁+ C₂ * q₂ = 10*500 + 20*440 =13800 у.е.

Как видно из полученного решения, L₁, равное 14117,65 у.е., больше чем Lопт, равное 13800 у.е., на 317,65 у.е. Это означает, что загрузка судна по Lопт менее выгодна, так как грузовместимость используется полностью, а грузоподъемность еще остается в запасе, что и отражается на величине дохода.

Определяющим ограничением в нашем случае является Q_1max = 500 т. Если его исключить, то можно подобрать такое решение, при котором можно принять на борт такое сочетание груза q₁ и q₂, чтобы добиться оптимального использования грузовместимости и грузоподъемности.

Максимально возможное значение целевой функции без ограничений находится в точке В, при q₁=588,235т и q₂=411,465т, то есть в том случае когда мы оптимально используем и грузовместимость и грузоподъемность судна. Значение целевой функции в точке В:

L=14117,65 у.е.

При увеличении или уменьшении стоимости С₁ и С₂ в 10-ть раз (С₁ = 100 у.е. и 1 у.е., С₂ = 200 у.е. и 2 у.е.) наклон прямой Lопт заметно не изменится, следовательно, найвыгоднейшие условия загрузки будут описываться прежней точкой ОДР и величины q_o1 и q_o2 останутся прежними, изменится лишь значение Lопт.

При С₁ = 100 у.е. и С₂ = 200 у.е.: Lопт_увел. = 100*500 + 200*440 = 138000 у.е.

При С₁ = 1 у.е. и С₂ = 2 у.е.: Lопт_умен. = 1*500 + 2*440 = 1380 у.е.

При перемене стоимости С₁ и С₂ наоборот, то есть С₁ = 20 у.е. и С₂ =10 у.е. наклон прямой Lопт изменится и значение целевой функции возрастет до

Lопт = C₁ *q_o1 + C₂ *q_o2 = 20*500 + 10*440 = 14400 у.е.

Графическое решение задачи представлено на рис.3.