Основным и важным понятием, науки теории вероятности является термин «случайного события».
Случайным событием (или просто: событием) называется любой исход опыта, который может произойти или не произойти.
Операции над событиями можно проиллюстрировать с помощью диаграмм Эйлера-Венна на рис.1:
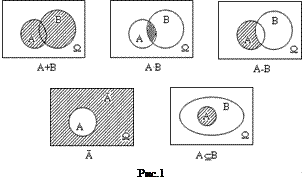 |
Операции над событиями обладают следующими свойствами:
▪ А+В=В+А, А∙В=В∙А (переместительное);
▪ (А+В)∙С=А∙С+В∙С, А∙В+С=(А+С)∙(В+С) ( распределительное);
▪ (А+В)+С=А+(В+С), (А∙В)∙С=А∙(В∙С) (сочетательное);
▪ А + А = А, А ∙ А = А;
▪ А + Ω = Ω, А ∙ Ω = А;
- 3 -
▪ А + 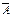 = Ω, А ∙
= Ω, А ∙ 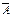 = Æ;
= Æ;
▪ 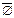 = Ω, Ω = Æ,
= Ω, Ω = Æ, 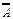 = А;
= А;
▪ А - В = А ∙ 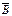 ;
;
▪ 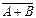 =
= 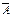 ∙
∙ 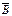 и
и 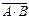 =
= 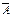 +
+ 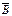 — законы де Моргана.
— законы де Моргана.
Например, рассмотрим опыт: бросание игральной кости; событие А — выпадение 5 очков, событие В — выпадение четного числа очков, событие D — выпадение целого числа очков, событие Е — выпадение не менее 3-х очков. Эти события будут состоять из следующих из элементов В ={2, 4, 6}, Е ={3, 4, 5, 6}, А ={5}, D ={1, 2, 3, 4, 5, 6}.
Тогда: В + Е = {2, 3, 4, 5, 6}, B ∙ E = {4, 6}, В - Е ={2}. Противоположным событию A будет событие 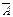 состоящее из следующих элементов
состоящее из следующих элементов 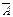 = {1, 2, 3, 4, 6}, событию В Í D, так как D = {1, 2, 3, 4, 5, 6}, то есть D= Ω.
= {1, 2, 3, 4, 6}, событию В Í D, так как D = {1, 2, 3, 4, 5, 6}, то есть D= Ω.
Пример. Доказать формулу А + В = А + 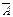 В.
В.
Решение. Используя некоторые из выше приведенных правил, получаем: А+В = (А + В) ∙ Ω = А∙Ω + В∙Ω= A∙Ω + B∙ (A+ 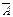 ) = А∙Ω + (А+
) = А∙Ω + (А+ 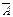 ) ∙В = A∙Ω + A∙B +
) ∙В = A∙Ω + A∙B + 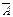 ∙B = (Ω + B) ∙A +
∙B = (Ω + B) ∙A + 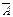 ∙B = Ω∙A +
∙B = Ω∙A + 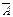 ∙B = A +
∙B = A + 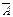 ∙В.
∙В.
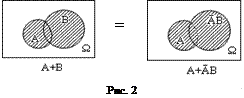
Таким образом, сумму любых двух событий можно представить в виде суммы двух несовместных событий.
Геометрическое доказательство представлено на рис. 2.
 |
 2015-06-10
2015-06-10 620
620







