Методы поиска

Численные методы поиска экстремальных значений функции рассмотрим на примере нахождения минимума функции 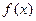на отрезке [а., b]. Будем предполагать, что целевая функция унимодальна, т.е. на данном отрезке она имеет только один минимум. Отметим, что в инженерной практике обычно встречаются именно такие целевые функции.

Погрешность приближенного решения задачи определяется разностью между оптимальным значением x проектного параметра и приближение к нему х. Потребуем, чтобы эта погрешность была по модулю меньше заданного допустимого значения а:

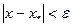(2.1)

Процесс решения задачи методом поиска состоит в последовательном сужении интервала изменения проектного параметра, называемого интервалом неопределенности. В начале процесса оптимизации его длина равна 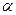, а к концу она должна стать меньше 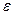, т. е. оптимальное значение проектного параметра должно находиться в интервале неопределенности – на отрезке 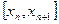, причем 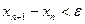. Тогда для выполнения (2.1) в качестве приближения к оптимальному значению можно принять любое .

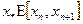Наиболее простым способом сужения интервала является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Пусть - число элементарных отрезков, 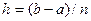- шаг разбиения. Вычислим значения целевой функции 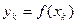в узлах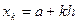 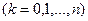. Сравнивая полученные значения 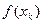, найдем среди них наименьшее .

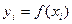Число 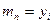можно приближенно принять за наименьшее значение целевой функции 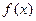на отрезке 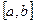. Очевидно, что близость 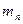к минимуму 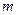зависит от числа точек, и для непрерывной функции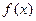

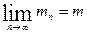
т. е. с увеличением числа точек разбиения погрешность минимума стремится к нулю.

В данном методе, который можно назвать методом перебора, главная трудность состоит в выборе 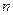и оценке погрешности. Можно, например, провести оптимизацию с разными шагами и исследовать сходимость такого итерационного процесса. Но это трудоемкий путь.

Более экономичным способом уточнения оптимального параметра является использование свойства унимодальности целевой функции, это позволяет построить процесс сужения интервала неопределенности. Пусть, как и ранее, среди всех значений унимодальной функции 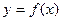, вычисленных в узлах 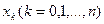наименьшим оказалось 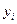. Это означает, что оптимальное значение проектного параметра находится на отрезке 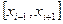, т. е. интервал неопределенности сузился до длины двух шагов. Если размер интервала недостаточен для удовлетворения заданной погрешности, т. е. ,

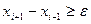то его снова можно уменьшить путем нового разбиения. Получится интервал, равный двум длинам нового шага разбиения и т. д. Процесс оптимизации продолжается до достижения заданного размера интервала неопределенности.

Существует ряд специальных методов поиска оптимальных решений разными способами выбора узлов и сужения интервала неопределенности - метод деления отрезка пополам, метод золотого сечения и др. Рассмотрим один из них.