Метод золотого сечения

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений (или измерений — при проведении эксперимента) значений целевой функции 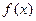. Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений 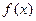достигается наилучшая точность, является метод золотого сечения. Он состоит в построении последовательности отрезков 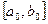, ,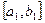..., стягивающихся к точке минимума функции 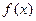. На каждом шаге, за исключением первого, вычисление значения функции 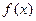проводится лишь в одной точке. Эта точка, называемая золотым сечением, выбирается специальным образом.

Поясним сначала идею метода геометрически, а затем выведем необходимые соотношения. Па первом шаге процесса оптимизации внутри отрезка 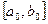выбираем некоторые внутренние точк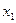и и 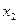и вычисляем значения целевой функци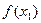и и 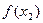. Поскольку в данном случае 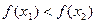, очевидно, что минимум расположен на одном из прилегающих к 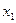отрезков: 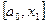или 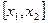. Поэтому отрезок 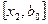можно отбросить, сузив тем самым первоначальный интервал неопределенности.

Второй шаг проводим на отрезк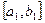е , где 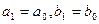. Нужно снова выбрать две внутренние точки, но одна из них 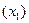осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку 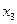, вычислить значение 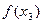и провести сравнение. Поскольку здесь 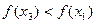, ясно, что минимум находится на отрезке 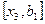. Обозначим этот отрезок 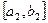, снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезка 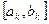не станет меньше заданной величины .

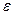Теперь рассмотрим способ размещения внутренних точек на каждом отрезке 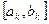. Пусть длина интервала неопределенности равна l, а точка деления разбивает его на части 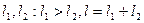. Золотое сечение интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка:

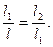(2.2)

Из этого соотношения можно найти точку деления, вычислив отношения

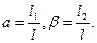
Преобразуем, выражение (2.2) и найдем значения ,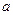

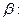
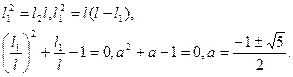
Поскольку пас интересует только положительное решение, то

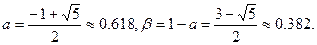
Очевидно, что интервал неопределенности можно разделить в соотношении золотого сечения двояко: в пропорциях 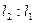и 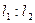. Точки деления 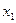и 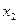выбираются с учетом этих пропорций. В данном случае имеем

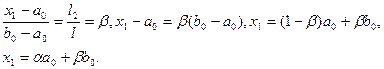(2.3)

Аналогично,

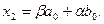(2.4)

Начальная длина интервала неопределенности составляет 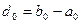. После первого шага оптимизации получается новый интервал неопределенности — отрезок 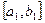. Его длина с учетом (2.4) равна

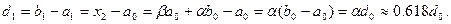
На втором шаге отрезок 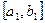также делится в соотношении золотого сечения. При этом одной из точек деления будет точка 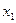. Покажем это:

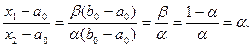
Последнее равенство следует из соотношения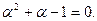

Вторая точка деления 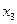выбирается так же, как выбирается точка 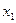при деления отрезка 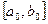, т. е. аналогично (2.3): 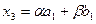. И снова интервал неопределенности уменьшается до размера

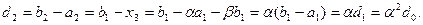
По аналогии с соотношениями (2.3), (2.4) можно записать координаты точек деления 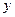и 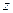отрезка 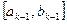на k-м шаге оптимизация :

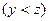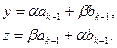
Вычислению, естественно, подлежит только одна из координат 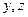; другая координата берется с предыдущего шага. При этом длина интервала неопределенности равна

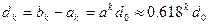(2.5)

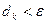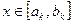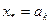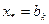Как я в общем случае метода поиска, процесс оптимизации заканчивается при выполнении условия . Тогда проектный параметр оптимизации . В качестве приближения к оптимальному значению можно принять или , или 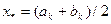. В последнем случае для достижения требуемой точности (для выполнения равенства) (2.1) достаточно, чтобы

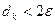(2.6)

Метод золотого сечения (как и, например, метод решения нелинейных уравнений делением отрезка пополам) относится к тем немногим численным методам, для которых можно гарантировать, что требуемая точность достигнута.