Метод покоординатного спуска

Пусть требуется найти наименьшее значение целевой функции 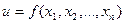. В качестве приближения выберем в 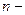мерном пространстве некоторую точку 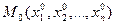. Зафиксируем все координаты функции 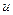, кроме первой. Тогда 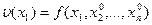фукция одной переменной 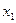. Первый шаг процесса оптимизации состоит в спуске по координате 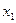в направлении убывания функции 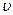от точки 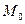до некоторой точки 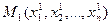. Если функция 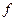дифференцируемая, то значение 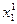может быть найдено

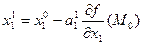(3.2)

Зафиксируем теперь все координаты кроме 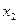, и рассмотрим функцию при переменной 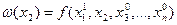. Снова осуществляем спуск теперь по координате 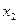, в сторону убывания функции 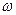от точки 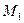до точки 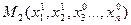. Значение 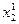можно найти

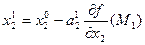
Аналогично проводится спуск по координатам 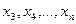, а затем процедура снова повторяется от 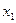до 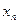. В результате этого процесса получается последовательность точек 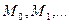, в которых значения целевой функции составляют монотонно убывающую последовательность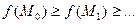

На любом k-том шаге этот процесс можно прервать. И значение функции в точке k принимается в качестве наименьшего значения целевой функции в рассматриваемой области.

Метод покоординатного спуска сводит задачу о нахождении наименьшего значения функции многих переменных к многократному.