Подходы имитационного моделирования на шкале абстракции

Агентное моделирование — относительно новое (1990-е-2000-е гг.) направление в имитационном моделировании, которое используется для исследования децентрализованных систем, динамика функционирования которых определяется не глобальными правилами и законами (как в других парадигмах моделирования), а наоборот, когда эти глобальные правила и законы являются результатом индивидуальной активности членов группы. Цель агентных моделей — получить представление об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении ее отдельных активных объектов и взаимодействии этих объектов в системе. Агент — некая сущность, обладающая активностью, автономным поведением, может принимать решения в соответствии с некоторым набором правил, взаимодействовать с окружением, а также самостоятельно изменяться.

Дискретно-событийное моделирование — подход к моделированию, предлагающий абстрагироваться от непрерывной природы событий и рассматривать только основные события моделируемой системы, такие как: «ожидание», «обработка заказа», «движение с грузом», «разгрузка» и другие. Дискретно-событийное моделирование наиболее развито и имеет огромную сферу приложений — от логистики и систем массового обслуживания до транспортных и производственных систем. Этот вид моделирования наиболее подходит для моделирования производственных процессов. Основан Джеффри Гордоном в 1960-х годах.

Системная динамика — парадигма моделирования, где для исследуемой системы строятся графические диаграммы причинных связей и глобальных влияний одних параметров на другие во времени, а затем созданная на основе этих диаграмм модель имитируется на компьютере. По сути, такой вид моделирования более всех других парадигм помогает понять суть происходящего выявления причинно-следственных связей между объектами и явлениями. С помощью системной динамики строят модели бизнес-процессов, развития города, модели производства, динамики популяции, экологии и развития эпидемии. Метод основан Джеем Форрестером в 1950 годах.

Вопрос

Критерий – это показатель или правило, с помощью которых различные варианты решений располагаются в порядке их желательности и выделяются наиболее предпочтительные из них.

Критерий – это некоторая функция от принятого решения, которая позволяет количественно оценить его целесообразность.

Критерии используются на разных этапах принятия решений: при ранжировании целей, оценке уровня их достижений; выборе и определении эффективности используемых при этом средств; при распределении ресурсов.

Выбор правильного критерия предопределяет результаты оценки различных вариантов решений.

Используемые в системном анализе критерии можно классифицировать на:

1) «оптимизационные» (наилучший вариант решения соответствует максимальному или минимальному значению этого критерия);

2) «ограничительные», вводимые для того, чтобы установить диапазон желаемых значений важнейших характеристик системы и исключить варианты решения, по которым хотя бы одна характеристика не попадает в требуемый диапазон.

Математическое выражение критерия оптимальности называют также целевой функцией, поскольку экстремум критерия является математическим отображением поставленной цели.

Среди оптимизационных критериев, в свою очередь, можно выделить: простые, состоящие из одного показателя, например прибыль, себестоимость; составные, включающие в свой состав несколько показателей, например критерии типа «стоимость – эффективность». Эти критерии основаны на разносторонней оценке затрат и результатов. Они могут включать не только измерение технико-экономических показателей, но и социальные последствия того или иного решения.

Взвешивающие критерии могут быть построены в виде определяемых экспертно величин предпочтительности сочетаний различных значений отдельных показателей. В этих целях для сочетания значений показателей, характеризующих возможные варианты решений (например, варианты плана), указывается, какое из сочетаний наиболее желательно.

При построении взвешивающих критериев используются экспертные оценки со всеми их недостатками, хотя для многих задач системного анализа, плохо поддающихся формализации, это единственный способ построения критерия.

Критерий должен быть представительным; критичным (чувствительным) к изменению исследуемых параметров; по возможности простым.

Представительность критерия означает оценку основных (а не второстепенных) целей системы и учет всех главных сторон ее деятельности.

Критичность (эластичность) к исследуемым параметрам состоит в значительных изменениях величины критерия при сравнительно малых изменениях исследуемых параметров. Высокая критичность в ряде случаев облегчает проведение математических исследований.

Простота прежде всего предполагает ясность смысла критерия, единиц его измерения.

Вопрос

ЛИНЕЙНЫЕ ОПЕРАТОРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЙ ЛАПЛАСА

Исследуемые модели относятся к классу линейных. Они описываются системой линейных интегро-дифференциальных уравнений. Блок схемы моделей состоят из скалярных векторов и линейных операторов, отображающих эти уравнения. Вектора и операторы преобразования представляют функции изображения, получаемые на основе преобразования временной функции по формуле прямого преобразования Лапласа [3]. Аргументом функции изображения является ком­плексная переменная s:

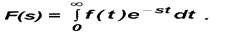
Функция f(t) вычисляется по формуле обратного пре­образования Лапласа:

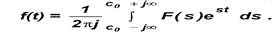
Каждой функции F(s) соответствует функция оригина­ла f(t). Соответствие функции изображения F(s) функ­ции оригинала f(t) обозначается с помощью знака соот­ветствия (*):

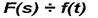(4) или, что то же

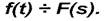(5)

В литературе применяется также другая форма запи­си преобразования Лапласа. Прямое преобразование записывается в виде:

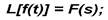(6) обратное преобразование Лапласа в виде:

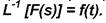(7)

Операторы преобразования на основе функции изо­бражения по Лапласу представляют передаточную функцию W(s) от комплексной переменной s. Переда­точной функцией называется отношение изображения по Лапласу выходной величины y(s) операторного зве­на к изображению входной величины x(s) при нулевых начальных условиях.

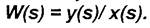(8)

Графически преобразование соответствующее (8) может быть представлено в виде блок-схемы, пред­ставленной на рис. 2.

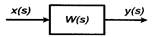
Рис. 2. Блок-схема преобразования функций изображения x(s) в y(s)

Величина y(s) на рис. 2 вычисляется путем простого перемножения:

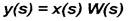(9)

Если известны входная функция x(s) т x(t) и переда­точная функция изображения W(s), оригинал функции y(t) может быть вычислен по формуле (10)

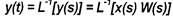
Для решения прикладных аналитических задач опре­деление оригинала y(t) осуществляется с помощью таблиц операционных соответствий, которые, как пра вило, достаточны для большинства прикладных задач моделирования. Минимальный перечень таких соответ­ствии, достаточный для исследуемых в работе моде­лей, представлен в приложении 1.

Вопрос

ЭЛЕМЕНТАРНЫЕ ОПЕРАТОРЫ

К элементарным операторам отнесем минимальный набор простейших передаточных функции изображе­ний, необходимых для построения структурных блок-схем экономических объектов. Такими звеньями явля­ются:

оператор пропорционального преобразования;

оператор дифференцирования;

оператор интегрирования;

оператор чистого запаздывания;

оператор суммирования. Этих операторов достаточно, чтобы отразить в про­странстве изображений по Лапласу все линейные пре­образования с временными функциями оригиналами. Ниже приведем описание этих операторов и указаны возможные объекты их применения для моделирования экономических процессов.

Оператор пропорционального преобразования

Оператор пропорционального преобразования отра­жает операцию умножения функции оригинала x(t) на постоянное действительное число к: y(t) = kx(t). В про­странстве изображений эта операция запишется виде равенства: y(s) = kx(s). Графически операция отража­ется в виде блок схемы на рис. 3.

Рис. 3. Блок-схема операции пропорционального преобразования

Примеры объектов применения:

• входной вектор - прибыль предприятия, оператор - про­цент налогообложения, выходной вектор - налоговые пла­тежи;

• входной вектор - ресурсы предприятия, оператор - частота оборачиваемости, выходной вектор - поток ресурсов;

• входной вектор - активы банка, оператор - доходность ак­тивов в %/год, выходной вектор - поток доходов.

Оператор дифференцирования

Оператор преобразует x(t) в выходной вектор y(t) в соответствии с уравнением: y(t)=dx(t)/dt. В пространст­ве изображений оператор дифференцирования W(s)=s, следовательно, операция запишется в соответствии с (9) в виде y(s) = sx(s). Блок-схема преобразования с оператором дифференцирования показана на рис. 4.

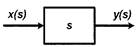
Рис. 4. Блок-схема операции дифференцирования

Примеры объектов применения:

> входной вектор - оборотные средства, выходной вектор -поток расходов оборотных средств;

входной вектор - денежные остатки на расчетном счете, выходной вектор - поток платежей с расчетного счета (при допущении непрерывного характера потоков

Вопрос

ТИПОВЫЕ СХЕМЫ СОЕДИНЕНИЯ ОПЕРАТОРОВ