1.1 Описание метода
Электрон – это элементарная частица с отрицательным электрическим зарядом, входящая в состав всех атомов, а следовательно, и любого обычного вещества. Это – самая легкая из электрически заряженных частиц. Электроны участвуют почти во всех электрических явлениях. В металле часть электронов не связана с атомами и может свободно перемещаться, благодаря чему металлы хорошо проводят электричество. В плазме, т.е. ионизованном газе, положительно заряженные атомы также перемещаются свободно, но, имея гораздо большую массу, движутся значительно медленнее электронов, а потому вносят меньший вклад в электрический ток. Благодаря малой массе электрон оказался частицей, наиболее вовлеченной в развитие квантовой механики, частной теории относительности и их объединение – релятивистскую квантовую теорию поля. Считается, что в настоящее время полностью известны уравнения, описывающие поведение электронов во всех реально осуществимых физических условиях (рисунок 1).
Рисунок 1 – Электрон
Удельным зарядом частицы называется физическая величина, равная отношению заряда частицы к её массе – q/m. Соответственно, удельный заряд электрона, это физическая величина, равная отношению заряда электрона к его массе – e/m. Удельный заряд определяют, изучая движение частиц в электрическом и магнитном полях. Одним из методов нахождения удельного заряда электрона может служить метод Чайлда-Ленгмюра. Он основан на измерении вольтамперной характеристики вакуумного диода, то есть зависимости анодного тока диода Ia от напряжения между катодом и анодом Ua.
Электрический ток переносится электронами, испускаемыми накалённым катодом. При малых напряжениях Ua анодный ток пропорционален Ua3/2. Эту зависимость называют законом «трёх вторых» или законом Чайлда-Ленгмюра.
1.3 Вывод формулы удельного заряда электрона
При некотором критическом значении индукции Вкр. траектория движения искривляется настолько, что она только касается анода. При В>Вкр. электроны совсем не достигают анода.
Радиус траектории электрона при В = Вкр. для лампы с достаточно тонким катодом равен половине радиуса анода, т.е.. Электрическое поле между катодом и анодом, перемещая электрон, совершает работу, вследствие чего электрон приобретает кинетическую энергию:
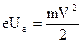 ,
,
где -Uа анодное напряжение. Из (1) и (2) с учетом того, что 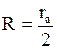 следует
следует 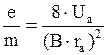 .Для соленоида
.Для соленоида 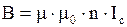 , здесь
, здесь 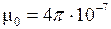 Гн/м магнитная постоянная;
Гн/м магнитная постоянная; 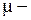 магнитная проницаемость воздуха, равная 1;
магнитная проницаемость воздуха, равная 1; 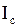 - сила тока в соленоиде;
- сила тока в соленоиде; 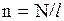 - число витков на единицу длины соленоида. С учетом этого окончательно имеем
- число витков на единицу длины соленоида. С учетом этого окончательно имеем
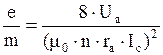
1.4. Пример приближенного вычисления удельного заряда электрона.
Метод магнетрона
Значение 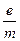 может быть найдено по траектории электрона в заданном магнитном и электрическом полях. На этом основаны многочисленные методы определения отношения заряда к массе для заряженных элементарных частиц. Точность данных методов определяется, в основном, точностью определения параметров траектории.
может быть найдено по траектории электрона в заданном магнитном и электрическом полях. На этом основаны многочисленные методы определения отношения заряда к массе для заряженных элементарных частиц. Точность данных методов определяется, в основном, точностью определения параметров траектории.
Одним из методов является метод магнетрона, в котором используется движение заряженной частицы во взаимно перпендикулярных магнитном и электрическом полях. Магнетрон представляет собой цилиндрический диод, помещенный в продольное магнитное поле. В отсутствие магнитного поля электроны, вылетающие с поверхности катода 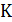 , движутся к аноду
, движутся к аноду  прямо по радиусам (рис 2, а).
прямо по радиусам (рис 2, а).
Магнитное поле действует на движущийся электрон с силой Лоренца:
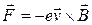 , (3)
, (3)
которая всегда перпендикулярна направлению вектора скорости 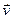 . Сила Лоренца не совершает работы, а может только повернуть вектор скорости, искривляя траекторию движения. Поэтому при включении магнитного поля траектории электронов в диоде начинают искривляться и приобретают более сложный характер, начинаясь на катоде и кончаясь на аноде. При определенном критическом значении магнитной индукции
. Сила Лоренца не совершает работы, а может только повернуть вектор скорости, искривляя траекторию движения. Поэтому при включении магнитного поля траектории электронов в диоде начинают искривляться и приобретают более сложный характер, начинаясь на катоде и кончаясь на аноде. При определенном критическом значении магнитной индукции 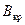 электроны совсем перестанут достигать анода (и анодный ток через диод прекратится (участок 3 ломаной сплошной линии на рисунок 2, б).
электроны совсем перестанут достигать анода (и анодный ток через диод прекратится (участок 3 ломаной сплошной линии на рисунок 2, б).
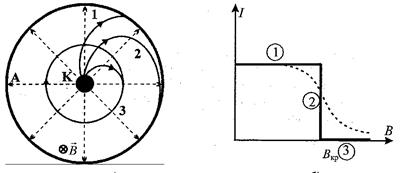
Рисунок 2.а – траектория электронов в магнетроне: 1-В < Bкр; 2-В=Вкр; 3-В>Вкр; А-анод, К-катод; поле В направлено от нас; б – зависимости анодного тока от магнитного поля: идеализированная – ломанная сплошная линия и реальная для исследуемого вакуумного диода – пунктирная линия
При 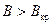 электроны образуют объемный отрицательный заряд, который вращается в пространстве между катодом и анодом, но сила анодного тока при этом близка к нулю. Таким образом, в данном методе сами траектории электронов не измеряются, но косвенно, по скачку анодного тока, фиксируется выход электронов на критическую траекторию с известными заранее параметрами. По параметрам этой траектории и рассчитывается удельный заряд
электроны образуют объемный отрицательный заряд, который вращается в пространстве между катодом и анодом, но сила анодного тока при этом близка к нулю. Таким образом, в данном методе сами траектории электронов не измеряются, но косвенно, по скачку анодного тока, фиксируется выход электронов на критическую траекторию с известными заранее параметрами. По параметрам этой траектории и рассчитывается удельный заряд 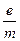 . Найдем величину критического поля. Ввиду аксиальной симметрии электродов рассмотрим движение электронов в цилиндрический координатах
. Найдем величину критического поля. Ввиду аксиальной симметрии электродов рассмотрим движение электронов в цилиндрический координатах 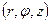 с началом в центре диода (рис. 3). По закону сохранения энергии скорость электрона у анода
с началом в центре диода (рис. 3). По закону сохранения энергии скорость электрона у анода 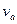 определяется пройденной им разностью потенциалов U между анодом и катодом:
определяется пройденной им разностью потенциалов U между анодом и катодом:
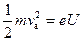 (4)
(4)
(считаем, что начальная скорость электрона равна нулю).
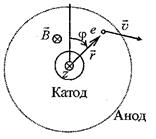
Рисунок 3. Цилиндрическая система координат
Момент импульса электрона 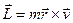 в нашей задаче имеет только z -составляющую. Рассмотрим ее изменение. При вылете из катода момент импульса электрона равен нулю (
в нашей задаче имеет только z -составляющую. Рассмотрим ее изменение. При вылете из катода момент импульса электрона равен нулю (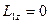 ). При критическом значении индукции
). При критическом значении индукции 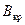 траектория электронов касается анода (кривая 2 на рис. 2, а). В точке касания момент импульса
траектория электронов касается анода (кривая 2 на рис. 2, а). В точке касания момент импульса
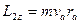 (5)
(5)
так как скорость направлена перпендикулярно радиусу. Изменение момента импульса электрона обусловлено только магнитной составляющей силы Лоренца, поскольку электрическая составляющая силы направлена по радиусу и ее момент всегда равен нулю. Момент силы Лоренца 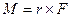 имеет только z -составляющую:
имеет только z -составляющую:
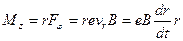 ,
,
где 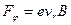 - азимутальная составляющая силы,
- азимутальная составляющая силы, 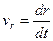 – радиальная составляющая скорости.
– радиальная составляющая скорости.
Закон изменения z -составляющей момента импульса имеет вид
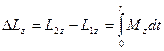 ,
,
где r – время полета электрона от катода до анода. Подставляя в него найденные выше соотношения, получаем.
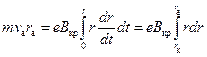 .
.
В последнем интеграле мы перешли к переменной интегрирования r и учли, что
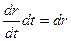
Интегрируя, получаем:
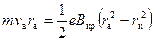 ,
,
где 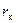 – радиус катода. Исключая
– радиус катода. Исключая 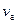 из (5) и (10), получаем связь между напряжением на диоде и критической индукцией магнитного поля:
из (5) и (10), получаем связь между напряжением на диоде и критической индукцией магнитного поля:
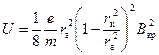 .
.
Если радиус катода мал по сравнению с радиусом анода (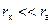 ), то из (11)
), то из (11)
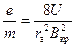 .
.
Однако, если учитывать объемный заряд вокруг катода(особенно при 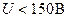 для используемого в данной работе вакуумного диода 3Ц18П), то нельзя пренебрегать величиной
для используемого в данной работе вакуумного диода 3Ц18П), то нельзя пренебрегать величиной 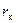 . Тогда расчетная формула будет:
. Тогда расчетная формула будет:
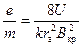
где поправочный коэффициент 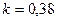 при
при 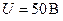 и
и 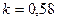 при
при 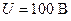 для данной установки.
для данной установки.
Таким образом, измерение критического поля 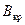 для заданного напряжения на диоде U дает возможность сразу найти
для заданного напряжения на диоде U дает возможность сразу найти 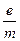 .
.
 2015-06-04
2015-06-04 5023
5023