Положение линии ЭПР в магнитном поле

Положение линии в магнитном поле определяется величиной 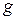-фактора, который является мерой эффективного магнитного момента электрона. В случае, если магнитный момент электрона соответствует чисто спиновому значению, 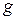-фактор равен 2,0023. Отклонение 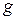-фактора от этой величины происходит вследствие вкладов в него, обусловленных взаимодействием спинового движения электрона 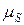с орбитальным 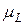, которые для разных веществ имеют различную величину. Поэтому 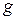-фактор является важной характеристикой индивидуального вещества, позволяющей идентифицировать вещества и судить об их электронном строении.

Для многих органических радикалов 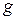-фактор вследствие малого вклада спин-орбитального взаимодействия близок к чисто спиновому значению. Однако поскольку он измеряется с высокой точностью, которая лимитируется лишь точностью определения абсолютных значений фундаментальных физических констант, то возможно использование 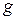-фактора для идентификации и более полной характеристики состояния неспаренного электрона в радикалах.

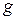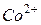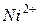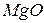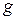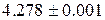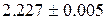В случае ионов переходных элементов -фактор сильно зависит от природы центрального иона. Например, и , введенные в качестве малой примеси в кубической симметрии, имеют соответственно -факторы и . Ион 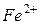в кристалле 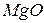октаэдрической симметрии имеет .

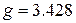Магнитные свойства парамагнитной частицы по разным направлениям пространства часто бывают различными. Поэтому 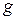-фактор может иметь несколько различных значений. Так, если лиганды, окружающие парамагнитную частицу, создают поле ромбической или более низкой симметрии, то частица имеет три 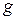-фактора: 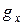, , 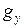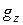. При аксиальной симметрии поля имеются два значения: 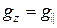и 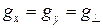. 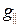-Фактор характеризует эффективный магнитный момент в направлении магнитного поля, a 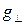– в плоскости 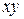, перпендикулярной к направлению поля.

Для дальнейшего рассмотрения введем понятия гамильтониана и спин-гамильтониана. Гамильтонианом 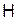называют полную энергию частицы, выраженную через импульс и координаты. Гамильтониан электрона в общем виде довольно сложен и состоит из следующих членов:

1) кинетической энергии электрона;

2) потенциальной энергии электрона, включающей и энергию взаимодействия с кристаллическим полем;

3) спин-орбитального взаимодействия. При движении электрона со скоростью 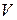в электрическом поле 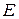экранированного ядра, находящегося от него на расстоянии 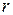, возникает магнитное поле

,

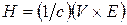которое взаимодействует со спиновым магнитным моментом 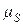, сообщая ему энергию ;

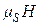4) взаимодействия электронного спинового 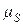и орбитального 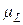моментов с внешним полем 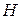, которое записывается в виде

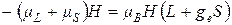(2.1)

5) магнитного взаимодействия ядерного спина с электронным спиновым и орбитальным моментами;

6) квадрупольного взаимодействия.

Предполагаем, что решение гамильтониана в отсутствие членов 3-6 известно. В этом разделе будем учитывать только спин-орбитальное взаимодействие и взаимодействие электронного и орбитального магнитных моментов с внешним магнитным полем. Гамильтониан этого взаимодействия имеет вид

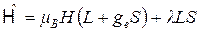(2.2)

Используя теорию возмущений, можно провести интегрирование выражения (2.2) по орбитальным переменным. Тогда гамильтониан (2.2) зависит только от спиновых переменных и равен

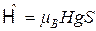(2.3)

Если бы не учитывалось спин-орбитальное взаимодействие, то вместо (2.3) получили бы

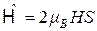(2.4)

Выражение (2.3) можно записать в виде

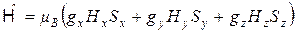(2.5)

где

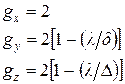(2.6)

Величины 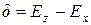и 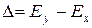представляют собой разности энергий основного 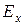и возбужденных 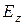, 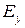состояний и находятся из оптических спектров.

Выражение (2.3) называют спин-гамильтонианом. Оно отличается от выражения (2.2) тем, что, как уже отмечалось, в нем проведено интегрирование по орбитальным переменным. Практическое удобство этого выражения заключается в том, что экспериментально находятся значения 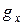, , 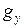, 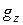с помощью которых описывается спектр.

Из выражений (2.2) и (2.3) видно, что совместное действие спин-орбитального и зеемановского взаимодействий эквивалентно замене реального поля 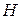эффективным полем .

,

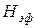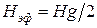которое отличается от приложенного по величине и направлению. Если ось 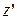новой системы координат выбрать в направлении эффективного поля, то, очевидно, при переходе к этой системе координат получим .

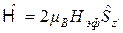Резонансная частота 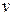определяется выражением

,

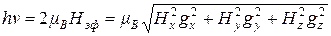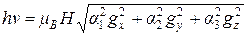(2.7)

где 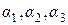– косинусы углов между 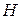и осями х, у, z.

Выражение (2.7) часто записывается в виде

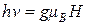, (2.8)

где

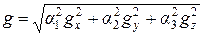. (2.9)

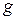-Фактор определяется экспериментально по известным 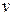и .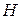

Анизотропия 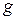-фактора определяется кристаллическим полем, создаваемым лигандами, окружающими парамагнитный ион. Поэтому парамагнитные спектры кристаллов являются средством изучения локальной симметрии парамагнитного иона, входящего в качестве примеси в решетку диамагнитного вещества. 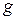-Фактор содержит, что не менее важно, большую информацию о характере связи парамагнитного атома (иона) с окружающими его лигандами, что подробно рассматривается в последующих разделах.