Дисперсия 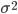 - представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
- представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.
Дисперсия простая:
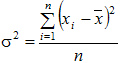
В нашем примере: 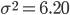
Дисперсия взвешенная:
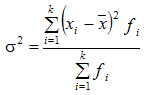
Более удобно вычислять дисперсию по формуле:
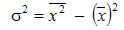
которая получается из основной путем несложных преобразований. В этом случае средний квадрат отклонений равен средней из квадратов значений признака минус квадрат средней.
Для несгрупиированных данных:
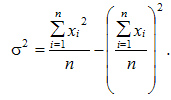
Для сгруппированных данных:
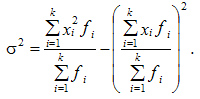
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой 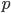 , а долю единиц, не обладающих этим признаком — через
, а долю единиц, не обладающих этим признаком — через 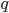 . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно
. Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно 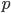
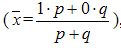 ,
,
средний квадрат отклонений
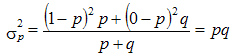
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (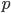 ), на долю единиц, данным свойством не обладающих (
), на долю единиц, данным свойством не обладающих (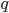 ).
).
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда 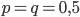 т.е.
т.е. 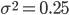 . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
. Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
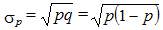
Так, если в изготовленной партии 3% изделий оказались нестандартными, то дисперсия доли нестандартных изделий 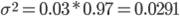 , а среднее квадратическое отклонение
, а среднее квадратическое отклонение 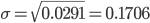 или 17,1%.
или 17,1%.
Среднее квадратическое отклонение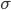 равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической.
равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической. 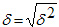
 2015-06-04
2015-06-04 567
567








