Расчет дисперсии по формуле по индивидуальным данным

Техника вычисления дисперсии сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.

Дисперсия имеет следующие свойства.

1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсию не изменяет.

2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсию не изменяет.

3. Уменьшение или увеличение каждого значения признака в какое-то число раз k соответственно уменьшает или увеличивает дисперсию в k ² раз, а среднее квадратическое отклонение ¾ в k раз.

4. Дисперсия признака относительно произвольной величины 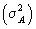всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величинами:

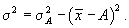
Если А = 0, то приходим к следующему равенству:

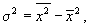
т. е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.

Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.

Порядок расчета дисперсии простой:

1) определяют среднюю арифметическую:

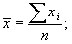
2) возводят в квадрат среднюю арифметическую:

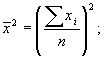
3) возводят в квадрат отклонение каждого варианта ряда:

х_i ².

4) находят сумму квадратов вариантов:

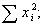
5) делят сумму квадратов вариантов на их число, т. е. определяют средний квадрат:

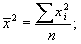
6) определяют разность между средним квадратом признака и квадратом средней:

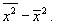
Пример 3.1 Имеются следующие данные о производительности труда рабочих:

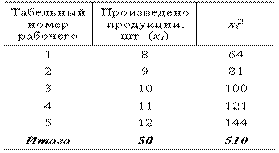
Произведем следующие расчеты:

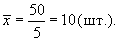
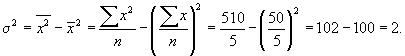
Рассмотрим расчет дисперсии в интервальном ряду распределения.

Порядок расчета дисперсии взвешенной (по формуле 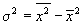) следующий:

1) определяют среднюю арифметическую:

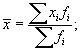
2) возводят в квадрат полученную среднюю:

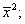
3) возводят в квадрат каждый вариант ряда:

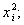
4) умножают квадраты вариантов на частоты:

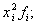
5) суммируют полученные произведения:

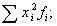
6) делят полученную сумму на сумму весов и получают средний квадрат признака:

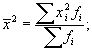
7) определяют разность между средним значением квадратов и квадратом средней арифметической, т. е. дисперсию:

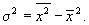
Пример 3.2 Имеются следующие данные о распределении посевной площади колхоза по урожайности пшеницы:

В подобных случаях прежде всего определяется дискретное значение признака в каждом интервале, а затем применяется рассмотренный метод расчета:

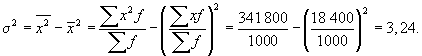
Средняя величина отражает тенденцию развития, т. е. действие главных причин. Среднее квадратическое отклонение измеряет силу воздействия прочих факторов.