Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к расстоянию между ее вершинами;обозначив эксцентриситет буквой 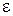 , получим:
, получим:
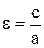
Так как для гиперболы с > а, то 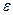 > 1; т. е. эксцентриситет каждой гиперболы больше единицы, Заметив, что
> 1; т. е. эксцентриситет каждой гиперболы больше единицы, Заметив, что 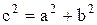 , находим:
, находим:
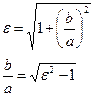
Следовательно, эксцентриситет определяется отношением 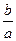 , а отношение
, а отношение 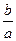 в свою очередь определяется эксцентриситетом. Таким образом,эксцентриситет гиперболы характеризует форму её основного прямоугольника, означит, и форму самой гиперболы.
в свою очередь определяется эксцентриситетом. Таким образом,эксцентриситет гиперболы характеризует форму её основного прямоугольника, означит, и форму самой гиперболы.
Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше 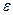 3-1, тем меньше, следовательно, отношение
3-1, тем меньше, следовательно, отношение 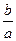 ; значит, чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник (в направлении оси, соединяющей вершины). В случае равносторонней гиперболы а = b и
; значит, чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник (в направлении оси, соединяющей вершины). В случае равносторонней гиперболы а = b и 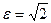 .
.
 2015-06-16
2015-06-16 5197
5197








