2015-06-04
2386
Теорема 1. Если любое выражение, входящее в уравнение, заменить тождественно равным ему на области определения уравнения выражением, то получим уравнение, равносильное данному.
Теорема 2. Если к обеим частям уравнения прибавить выражение, имеющее смысл на области определения уравнения, то получим уравнение, равносильное данному.
Следствие. Если любое слагаемое перенести из одной части уравнения в другую, поменяв его знак на противоположный, то получим уравнение, равносильное данному.
Теорема 3. Если обе части уравнения умножить (разделить) на выражение, имеющее смысл и отличное от нуля на области определения уравнения, то получим уравнение, равносильное данному.
Теорема 4. Уравнение
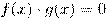
равносильно совокупности систем
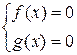
12. Критерий совместимости системы линейных уравнений (теорема Кронекера-Капелли).
Определение Системой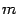 
линейных уравнений с 
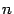неизвестными называется система уравнений вида
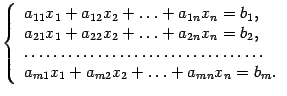(1)
Система уравнений называется однородной, если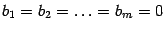 
и неоднородной в противном случае.
Определение Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной - в противном случае, то есть в случае, когда решений у системы нет.
Теорема (Теорема Кронекера-Капелли.) Система линейных уравнений (1) является совместной тогда и только тогда, когда ранг матрицы системы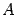 
равен рангу расширенной матрицы 
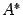. Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы. Если при этом ранг равен числу неизвестных, то система имеет единственное решение, если он меньше числа неизвестных, решений -множество.
Доказательство.
Оно распадается на два этапа. 1. Пусть система имеет решение. Покажем, что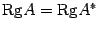 
. Ранг матрица А равен рангу расширенной матрицы.
Пусть набор чисел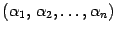 
является решением системы. Обозначим через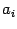 
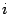-ый столбец матрицы , 
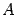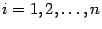. Тогда 
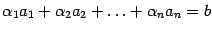, то есть столбец свободных членов является линейной комбинацией столбцов матрицы 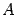. Пусть 
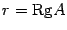. Предположим, что 
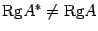. Тогда по предположению, что ранг расширенной матрицы 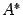либо равен рангу матрицы системы 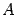, либо больше его на единицу запишем 
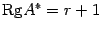. Выберем в 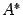базисный минор 
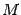. Он имеет порядок 
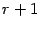. Столбец 
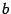свободных членов обязан проходить через этот минор, иначе он будет базисным минором матрицы 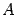. Столбец свободных членов в миноре 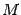является линейной комбинацией столбцов матрицы 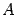. В силу некоторых свойств определителя, например все свойства определителя, сформулированные для строк, справедливы и для столбцов, в частности, справедливо разложение определителя по 
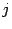-ому столбцу имеем 
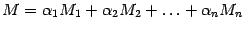, где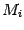 
- определитель, который получается из минора 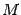заменой столбца свободных членов на столбец 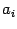. Если столбец 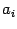проходил через минор 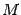, то в 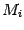, будет два одинаковых столбца и, следовательно, 
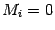. Если столбец 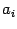не проходил через минор 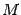, то 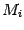будет отличаться от минора порядка 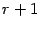матрицы 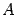только порядком столбцов. Так как 
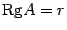, то 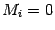. Таким образом, 
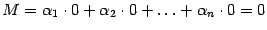, что противоречит определению базисного минора. Значит, предположение, что 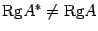, неверно.
2. Пусть 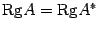. Покажем, что система имеет решение. Так как 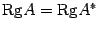, то базисный минор 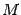матрицы 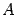является базисным минором матрицы 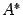. Пусть через минор 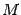проходят столбцы 
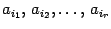. Тогда по теореме о базисном миноре в матрице 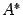столбец свободных членов является линейной комбинацией указанных столбцов: 
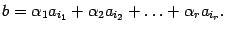(2)
Положим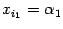 
, 
, 
, 
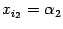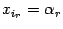, остальные неизвестные возьмем равными нулю. Тогда при этих значениях 
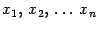получим
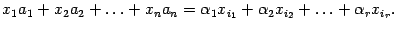
В силу равенства (2)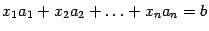 
. Последнее равенство означает, что набор чисел 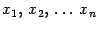является решением системы. Существование решения доказано.
В рассмотренной выше системе (1)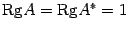 
, и система является совместной.
Замечание Хотя теорема Кронекера-Капелли дает возможность определить, является ли система совместной, применяется она довольно редко, в основном в теоретических исследованиях. Причина заключается в том, что вычисления, выполняемые при нахождении ранга матрицы, в основном совпадают с вычислениями при нахождении решения системы. Поэтому, обычно вместо того, чтобы находить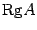 
и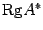 
, ищут решение системы. Если его удается найти, то узнаем, что система совместна и одновременно получаем ее решение. Если решение не удается найти, то делаем вывод, что система несовместна.
Пример. Исследовать систему линейных уравнений
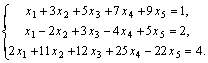
Решение. Поскольку все элементы матрицы системы входят в расширенную матрицу, то ранги обеих матриц можно вычислять одновременно.
~ 
~
~ 
.
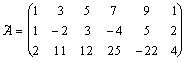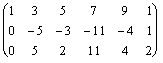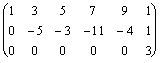Таким образом, матрица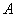 
содержит две ненулевые строки, значит ее ранг 
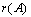равен двум. В матрице 
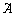три ненулевых строки, ее ранг 
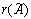равен трем. А т.к. 
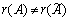, система несовместна.
13. Базис и размерность конечного векторного пространства.
Рассмотрим конечное векторное пространство.
Определение: Пространство называется n-мерным если в нем существует линейно независимая система состоящая из n-векторов, а любая система, состоящая из большего числа векторов всегда линейно зависима.
Бесконечное пространство, например: множество функций вида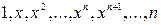 
-множество натуральных чисел.
Пример n-мерное пространство: пространство с расширением (диминейшен)3 и 2 (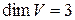
или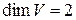 
)
Базисом n-мерного векторного пространства называется любая линейно независимая подсистема этой системы состоящая из n-элементов.
Следствие: Любые два базиса векторного пространства состоят из одинакового числа векторов (n-векторов, если n-мерное пространство).
Число векторов в любом базисе равно n, где n-размерность пространства.
Любая система из n-линейно независимых векторов является базисом, так как добавление к этой системе хотя бы одного вектора делает ее линейно зависимой.
Теорема: В конечном пространстве V любая система векторов, содержащая хотя бы один не нулевой вектор обязательно имеет базис.
